APMO 1997 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Olimpiadas > Olimpiada Asia-Pacifico

Reply to this topic

Start new topic

APMO 1997, Ssp: 2,3,4,5

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 25 2007, 08:11 PM Publicado: #1
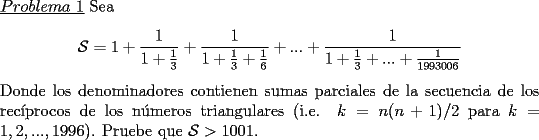Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent \underline{$Problema\ 1$} Sea\<br />\begin{center}<br />$\mathcal{S}=1+\dfrac{1}{1+\frac{1}{3}}+\dfrac{1}{1+\frac{1}{3}+\frac{1}{6}}+...+\dfrac{1}{1+\frac{1}{3}+...+\frac{1}{1993006}}$<br />\end{center}<br />Donde los denominadores contienen sumas parciales de la secuencia de los rec\'iprocos de los n\'umeros triangulares (i.e. $k=n(n+1)/2$ para $k=1,2,...,1996$). Pruebe que $\mathcal{S}>1001$.$ Solucion: $TEX: Si $n$ es un natural mayor que $1$ entonces <br /><br />$\medskip$<br /><br />$\displaystyle \frac{1}{n+1} + \frac{1}{n+2} + \ldots + \frac{1}{2n} > \frac{1}{2}.$<br /><br />$\medskip$<br /><br />Luego, al ser<br /><br />$\medskip$<br /><br />$\displaystyle \mathcal{S} = \frac{1}{2} \sum_{k=1}^{1996} \frac{k+1}{k} = 998 + \frac{1}{2} \sum_{k=1}^{1996} \frac{1}{k}$<br /><br />$\medskip$<br /><br />la desigualdad de arriba implica que<br /><br />$\medskip$<br /><br />$\displaystyle \sum_{k=1}^{1996} \frac{1}{k} > \sum_{k=1}^{2^{10}} \frac{1}{k} = \left(1+\frac{1}{2}\right) + \left(\frac{1}{3}+\frac{1}{2^{2}}\right) + \left(\frac{1}{5}+\ldots + \frac{1}{2^{3}}\right) + \ldots + \left(\frac{1}{513}+\ldots + \frac{1}{2^{10}}\right) > \left(1 + \frac{1}{2} \right) + \frac{9}{2} = 6$<br /><br />$\medskip$<br /><br />y sería. 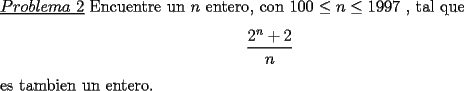$\textbf{QED}.$<br /><br />$ $TEX: \boxed{Resuelto\ por\ coquitao}$ $TEX: \noindent \underline{$Problema\ 2$} Encuentre un $n$ entero, con $100\le n\le 1997$ , tal que\<br />\begin{center}<br />$\dfrac{2^n+2}{n}$<br />\end{center}<br />es tambien un entero.$ Solucion: (Pendiente) $TEX: \noindent \underline{$Problema\ 3$} Sea $ABC$ un tri\'angulo inscrito en una circunferencia, y sea\<br />\begin{center}<br />$l_a=\dfrac{m_a}{M_a}$ , $l_b=\dfrac{m_b}{M_b}$ , $l_a=\dfrac{m_c}{M_c}$ ,<br />\end{center}<br />donde $m_a$, $m_b$, $m_c$ son las medidas de las bisectrices interiores, y $M_a$, $M_b$, $M_c$ son las medidas de las bisectrizes exteriores extendidas hasta que cortan la circunferencia. Pruebe que\<br />\begin{center}<br />$\dfrac{l_a}{sin^2A}+\dfrac{l_b}{sin^2B}+\dfrac{l_c}{sin^2C}\ge 3$,<br />\end{center}<br />y con igualdad si y solo si $ABC$ es equil\'atero.$ Solucion: (Pendiente) $TEX: \noindent \underline{$Problema\ 4$} El tri\'angulo $A_1A_2A_3$ es recto en $A_3$. Ahora se define una secuencia de puntos donde $n$ es un entero positivo. Desde $A_n$ ($n\ge 3$) se dibuja una perpendicular a $A_{n-1}A_{n-2}$ cuya intersecci\'on ser\'a $A_{n+1}$.\\<br />\\(a) Pruebe que si este proceso continua infinitamente, entonces uno y solo un punto $P$ se encuentra en el interior de cada tri\'angulo $A_{n-2}A_{n-1}A_n$, $n\ge 3$.\\<br />\\(b) Sean $A_1$ y $A_3$ puntos fijos. Considerando todos los lugares posibles de $A_2$ en el plano, encuentre el lugar geom\'etrico de $P$.$ Solucion: (Pendiente) $TEX: \noindent \underline{$Problema\ 5$} Suponga que $n$ personas $A_1,A_2,...,A_n$, ($n\ge 3$) son sentadas en un c\'irculo y que $A_i$ tiene $a_i$ objetos tales que\<br />\begin{center}<br />$a_1+a_2+...+a_n=nN$,<br />\end{center}<br />donde $N$ es un entero positivo. De forma tal que cada persona tenga el mismo n\'umero de objetos, cada persona $A_i$ da o recibe un cierto n\'umero de objetos a o desde sus dos vecinos $A_{i-1}$ y $A_{i+1}$. (Aqu\'i $A_{n+1}$ significa $A_1$ y $A_n$ significa $A_0$.) Explique como debe hacerse esta distribuci\'on de forma que la cantidad de objetos transferidos sea m\'inimo.$ Solucion: (Pendiente) Mensaje modificado por Luffy el Sep 26 2011, 11:10 PM

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 25 2007, 09:42 PM Publicado: #2
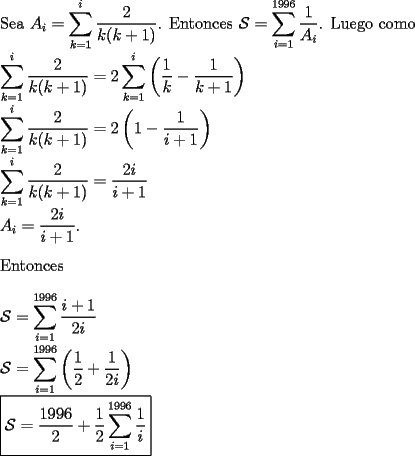Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: $\boxed{Sp_1}$$ $TEX: \noindent Sea $A_i=\displaystyle\sum_{k=1}^i\dfrac{2}{k(k+1)}$. Entonces $\mathcal{S}=\displaystyle\sum_{i=1}^{1996}\dfrac{1}{A_i}$. Luego como\\<br />$\displaystyle\sum_{k=1}^i\dfrac{2}{k(k+1)}=2\displaystyle\sum_{k=1}^i\left( \dfrac{1}{k}-\dfrac{1}{k+1}\right)$\\<br />$\displaystyle\sum_{k=1}^i\dfrac{2}{k(k+1)}=2\left(1-\dfrac{1}{i+1}\right)$\\<br />$\displaystyle\sum_{k=1}^i\dfrac{2}{k(k+1)}=\dfrac{2i}{i+1}$\\<br />$A_i=\dfrac{2i}{i+1}$.\\<br />\\Entonces\\<br />\\<br />$\mathcal{S}=\displaystyle\sum_{i=1}^{1996}\dfrac{i+1}{2i}$\\<br />$\mathcal{S}=\displaystyle\sum_{i=1}^{1996}\left( \dfrac{1}{2}+\dfrac{1}{2i}\right)$\\<br />$\boxed{\mathcal{S}=\dfrac{1996}{2}+\dfrac{1}{2}\displaystyle\sum_{i=1}^{1996}\dfrac{1}{i}}$$ $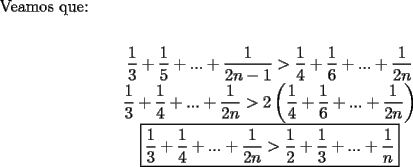TEX: \noindent Veamos que:\\<br />\begin{center}<br />$\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{2n-1}>\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2n}$\\<br />$\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2n}>2\left( \dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2n}\right)$\\<br />$\boxed{\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2n}>\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{n}}$<br />\end{center}$ $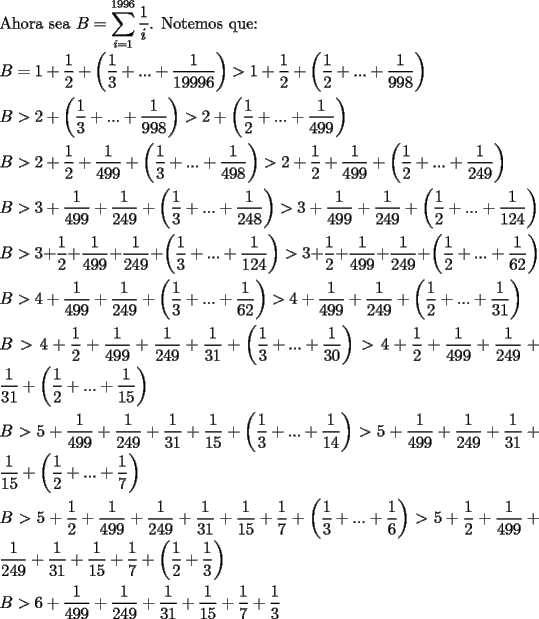TEX: \noindent Ahora sea $B=\displaystyle\sum_{i=1}^{1996}\dfrac{1}{i}$. Notemos que:\\<br />\\<br />$B=1+\dfrac{1}{2}+\left( \dfrac{1}{3}+...+\dfrac{1}{19996}\right)>1+\dfrac{1}{2}+\left( \dfrac{1}{2}+...+\dfrac{1}{998}\right)$\\<br />\\<br />$B>2+\left( \dfrac{1}{3}+...+\dfrac{1}{998}\right)>2+\left( \dfrac{1}{2}+...+\dfrac{1}{499}\right)$\\<br />\\<br />$B>2+\dfrac{1}{2}+\dfrac{1}{499}+\left( \dfrac{1}{3}+...+\dfrac{1}{498}\right)>2+\dfrac{1}{2}+\dfrac{1}{499}+\left( \dfrac{1}{2}+...+\dfrac{1}{249}\right)$\\<br />\\<br />$B>3+\dfrac{1}{499}+\dfrac{1}{249}+\left( \dfrac{1}{3}+...+\dfrac{1}{248}\right)>3+\dfrac{1}{499}+\dfrac{1}{249}+\left( \dfrac{1}{2}+...+\dfrac{1}{124}\right)$\\<br />\\<br />$B>3+\dfrac{1}{2}+\dfrac{1}{499}+\dfrac{1}{249}+\left( \dfrac{1}{3}+...+\dfrac{1}{124}\right)>3+\dfrac{1}{2}+\dfrac{1}{499}+\dfrac{1}{249}+\left( \dfrac{1}{2}+...+\dfrac{1}{62}\right)$\\<br />\\<br />$B>4+\dfrac{1}{499}+\dfrac{1}{249}+\left( \dfrac{1}{3}+...+\dfrac{1}{62}\right)>4+\dfrac{1}{499}+\dfrac{1}{249}+\left( \dfrac{1}{2}+...+\dfrac{1}{31}\right)$\\<br />\\<br />$B>4+\dfrac{1}{2}+\dfrac{1}{499}+\dfrac{1}{249}+\dfrac{1}{31}+\left( \dfrac{1}{3}+...+\dfrac{1}{30}\right)>4+\dfrac{1}{2}+\dfrac{1}{499}+\dfrac{1}{249}+\dfrac{1}{31}+\left( \dfrac{1}{2}+...+\dfrac{1}{15}\right)$\\<br />\\<br />$B>5+\dfrac{1}{499}+\dfrac{1}{249}+\dfrac{1}{31}+\dfrac{1}{15}+\left( \dfrac{1}{3}+...+\dfrac{1}{14}\right)>5+\dfrac{1}{499}+\dfrac{1}{249}+\dfrac{1}{31}+\dfrac{1}{15}+\left( \dfrac{1}{2}+...+\dfrac{1}{7}\right)$\\<br />\\<br />$B>5+\dfrac{1}{2}+\dfrac{1}{499}+\dfrac{1}{249}+\dfrac{1}{31}+\dfrac{1}{15}+\dfrac{1}{7}+\left( \dfrac{1}{3}+...+\dfrac{1}{6}\right)>5+\dfrac{1}{2}+\dfrac{1}{499}+\dfrac{1}{249}+\dfrac{1}{31}+\dfrac{1}{15}+\dfrac{1}{7}+\left( \dfrac{1}{2}+\dfrac{1}{3}\right)$\\<br />\\<br />$B>6+\dfrac{1}{499}+\dfrac{1}{249}+\dfrac{1}{31}+\dfrac{1}{15}+\dfrac{1}{7}+\dfrac{1}{3}$\\$ $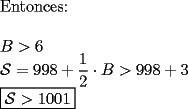TEX: \noindent Entonces:\\<br />\\<br />$B>6$\\<br />$\mathcal{S}=998+\dfrac{1}{2}\cdot B>998+3$\\<br />$\boxed{\mathcal{S}>1001}$<br />$

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 22 2010, 12:13 AM Publicado: #3
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	Pongo a su consideración mi vieja solución a 1. $TEX: Si $n$ es un natural mayor que $1$ entonces <br /><br />$\medskip$<br /><br />$\displaystyle \frac{1}{n+1} + \frac{1}{n+2} + \ldots + \frac{1}{2n} > \frac{1}{2}.$<br /><br />$\medskip$<br /><br />Luego, al ser<br /><br />$\medskip$<br /><br />$\displaystyle \mathcal{S} = \frac{1}{2} \sum_{k=1}^{1996} \frac{k+1}{k} = 998 + \frac{1}{2} \sum_{k=1}^{1996} \frac{1}{k}$<br /><br />$\medskip$<br /><br />la desigualdad de arriba implica que<br /><br />$\medskip$<br /><br />$\displaystyle \sum_{k=1}^{1996} \frac{1}{k} > \sum_{k=1}^{2^{10}} \frac{1}{k} = \left(1+\frac{1}{2}\right) + \left(\frac{1}{3}+\frac{1}{2^{2}}\right) + \left(\frac{1}{5}+\ldots + \frac{1}{2^{3}}\right) + \ldots + \left(\frac{1}{513}+\ldots + \frac{1}{2^{10}}\right) > \left(1 + \frac{1}{2} \right) + \frac{9}{2} = 6$<br /><br />$\medskip$<br /><br />y sería. $\textbf{QED}.$<br /><br />$ P.D. Unos metros más corta que la de Luffy, ¿no? -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 26 2011, 11:08 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(coquitao @ Apr 22 2010, 01:13 AM) Pongo a su consideración mi vieja solución a 1. $TEX: Si $n$ es un natural mayor que $1$ entonces <br /><br />$\medskip$<br /><br />$\displaystyle \frac{1}{n+1} + \frac{1}{n+2} + \ldots + \frac{1}{2n} > \frac{1}{2}.$<br /><br />$\medskip$<br /><br />Luego, al ser<br /><br />$\medskip$<br /><br />$\displaystyle \mathcal{S} = \frac{1}{2} \sum_{k=1}^{1996} \frac{k+1}{k} = 998 + \frac{1}{2} \sum_{k=1}^{1996} \frac{1}{k}$<br /><br />$\medskip$<br /><br />la desigualdad de arriba implica que<br /><br />$\medskip$<br /><br />$\displaystyle \sum_{k=1}^{1996} \frac{1}{k} > \sum_{k=1}^{2^{10}} \frac{1}{k} = \left(1+\frac{1}{2}\right) + \left(\frac{1}{3}+\frac{1}{2^{2}}\right) + \left(\frac{1}{5}+\ldots + \frac{1}{2^{3}}\right) + \ldots + \left(\frac{1}{513}+\ldots + \frac{1}{2^{10}}\right) > \left(1 + \frac{1}{2} \right) + \frac{9}{2} = 6$<br /><br />$\medskip$<br /><br />y sería. $\textbf{QED}.$<br /><br />$ P.D. Unos metros más corta que la de Luffy, ¿no? Muy bien, una mejor solucion pasa a las soluciones oficiales

« Posterior · Olimpiada Asia-Pacifico · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 3rd April 2025 - 09:16 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.