tres propuestos - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector PreOlímpico > Combinatoria > Problemas Resueltos

2 Páginas:

1 2 >

Reply to this topic

Start new topic

tres propuestos, no muy complicados

Felipe_ambuli Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 20 2007, 10:41 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad: Sexo:	$TEX: \noindent <br />i) El sistema de patentes de veh\'iculos consiste en un n\'umero de 4 d\'igitos\\<br />seguido de un bloque de 3 letras consonantes (Ej: 0474 - $KTK$)\\<br />\\<br />a) Cu\'antas placas hay con un determinado bloque de letras?\\<br />b) Cu\'antas placas hay con la misma parte num\'erica?\\<br />c) Cu\'antas placas se pueden formar en total con este sistema de patentes?\\<br />\\<br />\\<br />ii) Se va a celebrar la final de salto de longitud en un torneo de atletismo.\\<br />Participan 8 atletas. De cu\'antas formas pueden repartirse las tres medallas de oro, plata y bronce?\\<br />\\<br />\\<br />iii) En la primera ronda de un campeonato de ajedrez cada participante debe jugar contra todos los dem\'as una sola partida. Participan 23 jugadores.\\<br />Cuantas partidas se disputar\'an?\\<br />\\<br />Saludos$ Mensaje modificado por Felipe_ambuli el Sep 14 2007, 12:59 PM

julio el chato Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 27 2007, 06:56 PM Publicado: #2
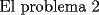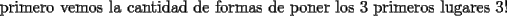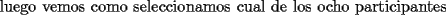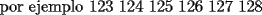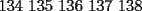Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 24 Registrado: 14-June 07 Desde: mi casa Miembro Nº: 6.722 Nacionalidad: Sexo:	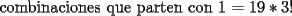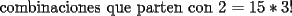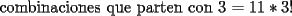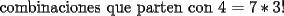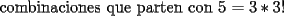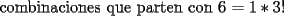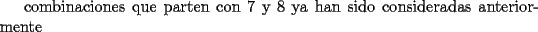$TEX: El problema 2$ $TEX: primero vemos la cantidad de formas de poner los 3 primeros lugares $3!$$ $TEX: luego vemos como seleccionamos cual de los ocho participantes$ $TEX: por ejemplo 123 124 125 126 127 128$ $TEX: 134 135 136 137 138$ $TEX: y notamos que se reduce en uno la anterior forma de combinaciones por lo que, los que comienzan con uno van a ser en total $19 x 3!$ luego las combinaciones que comienzan con 2 por ejemplo(234 235 236 237 238) van a ser en total 4 menos que las que parten con 1 por lo tanto$ $TEX: combinaciones que parten con 1 $=19 * 3!$$ $TEX: combinaciones que parten con 2 $=15 * 3!$$ $TEX: combinaciones que parten con 3 $=11 * 3!$$ $TEX: combinaciones que parten con 4 $=7 * 3!$$ $TEX: combinaciones que parten con 5 $=3 * 3!$$ $TEX: combinaciones que parten con 6 $=1 * 3!$$ $TEX: combinaciones que parten con 7 y 8 ya han sido consideradas anteriormente$ otra cosa como se hace el por xd 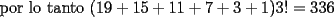$TEX: por lo tanto $(19+15+11+7+3+1)3!=336$$ -------------------- ola

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 28 2007, 10:57 AM Publicado: #3
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Entiendo tu razonamiento, pero cometiste un error en las cuentas. El 19 debiese ser 21, poqrue al elegir al atleta 1 tienes 21 posibilidades: 123 124 125 126 127 128 134 135 136 137 138 145 146 147 148 156 157 158 167 168 178 Con la misma idea, el 11 debe ser 10 y el 7 debe ser 6 En cualquier caso, 21+15+10+6+3+1 = 56, por eso tus cuentas llegaron al resultado correcto Por cierto, existe una solución muchísimo más breve, y que puedes aplicar en otros casos. De hecho, los tres problemas que propuso Felipe_ambuli, están para aprender lo más básico en combinatoria -------------------- Sebastián Elías Puelma Moya Administrador FMAT

julio el chato Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 28 2007, 05:02 PM Publicado: #4
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 24 Registrado: 14-June 07 Desde: mi casa Miembro Nº: 6.722 Nacionalidad: Sexo:	ok -------------------- ola

br1_001 Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 28 2007, 05:18 PM Publicado: #5
Matemático Grupo: Usuario FMAT Mensajes: 55 Registrado: 15-February 07 Desde: Avila; Castilla y León, España. Miembro Nº: 4.087 Nacionalidad: Sexo:	Alternativamente para el problema 2, se pudo usar la formula para las variaciones de "m" elementos de un conjunto, tomados de "n en n" (donde el orden de los elementos importa). En nuestro caso se tiene: $TEX: \[<br />\frac{{8!}}<br />{{\left( {8 - 3} \right)!}} = 336<br />\]$ -------------------- Remember when you were young, you shone like the sun...(Pink Floyd)

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 28 2007, 07:08 PM Publicado: #6
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	La respuesta es rápida y correcta. Sólo queda explicar, para quien no conociera previamente el concepto de permutación, cómo hacer esto Primero, entregaremos la medalla de oro. Debemos elegir a uno de los ocho atletas en competición. A continuación, entregaremos la medalla de plata. Como el medallista de oro no la puede recibir, entonces debemos elegir a uno de los siete atletas restantes. Finalmente, entregaremos la medalla de bronce. Como los medallistas de oro y plata no la pueden recibir, entonces debemos elegir a uno de los seis atletas restantes. Por lo tanto, la distribución de medallas consiste en tres procesos. De cuántas maneras se puede hacer esto? Aplicamos la regla del producto (esta parte es intuitiva, así que deben buscar una buena referencia, como el sector de contenidos de fmat, para aclarar dudas), para concluir que se puede hacer de 8 · 7 · 6 = 336 formas -------------------- Sebastián Elías Puelma Moya Administrador FMAT

Assassin.... Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 5 2007, 10:02 PM Publicado: #7
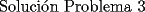Matemático Grupo: Usuario FMAT Mensajes: 45 Registrado: 20-October 07 Miembro Nº: 11.559 Nacionalidad: Sexo:	$TEX: Soluci\'on Problema 3$ $TEX: Llamemos $a_1, a_2, a_3, ..., a_{23}$ a los participantes. Supongamos que $a_1$ juega contra otros 22 jugadores de corrido en la primera ronda (ya que no puede jugar contra s\'i mismo), es decir juega 22 partidas. 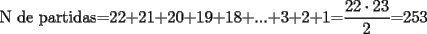$a_2$ juega 21 partidas de corrido ya que anteriormente hab\'ia jugado con $a_1$, de la misma manera $a_3$ juega 20 partidas, $a_4$ juega 19 partidas y as\'i sucesivamente hasta que $a_{22}$ juega 1 partida y $a_{23}$ ya jug\'o con todos, es decir se jugaron:$ $TEX: Nº de partidas=22+21+20+19+18+...+3+2+1=$\dfrac{22\cdot23}{2}$=253$ Mensaje modificado por Assassin.... el Nov 5 2007, 10:19 PM

Felipe_ambuli Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 5 2007, 10:12 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad: Sexo:	CITA(Assassin.... @ Nov 6 2007, 01:02 AM) $TEX: Soluci\'on Problema 2$ $TEX: Llamemos $a_1, a_2, a_3, ..., a_{23}$ a los participantes. Supongamosque $a_1$ juega contra otros 22 jugadores de corrido en la primera ronda (ya que no puede jugar contra s\'i mismo), es decir juega 22 partidas. $a_2$ juega 21 partidas de corrido ya que anteriormente hab\'ia jugado con $a_1$, de la misma manera $a_3$ juega 20 partidas, $a_4$ juega 19 partidas y as\'i sucesivamente hasta que $a_{22}$ juega 1 partida y $a_{23}$ ya jug\'o con todos, es decir se jugaron:$ $TEX: Nº de partidas=22+21+20+19+18+...+3+2+1=$\dfrac{22\cdot23}{2}$=253$ Asi de simple... correcto, solo acotar que es el iii) y no el ii). Animense para el i) Saludos EDITED: Identidad de Assassin... oculta xD Mensaje modificado por Felipe_ambuli el Nov 5 2007, 10:20 PM

Assassin.... Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 5 2007, 10:35 PM Publicado: #9
Matemático Grupo: Usuario FMAT Mensajes: 45 Registrado: 20-October 07 Miembro Nº: 11.559 Nacionalidad: Sexo:	$TEX: Soluci\'on Problema 1$ $TEX: a) Si tenemos un "determinado bloque de letras" no influye en el n\'umero de combinaciones finales. Entonces nos queda que: en la primera casilla podemos colocar 10 n\'umeros distinos, en la segunda, en la tecera y en la cuarta tambi\'en ya que los n\'umeros se pueden repetir. Es decir en este caso tenemos $10\cdot10\cdot10\cdot10$=$10^4$=10000 combinaciones$ $TEX: b) Al igual que en el problema anterior si tenemos un "determinado bloque de n\'umeros" no influye en el n\'umero final de combinaciones. Entonces tenemos que: en la primera casilla podemos colocar 22 consonantes distintas, en la segunda y en la tercera tambi\'en, as\'i que se forman:$ 22\cdot22\cdot22$=$22^3$=10648 combinaciones$ $TEX: c) En este caso basta multiplicar el n\'umero de combinaciones posibles con n\'umeros con el n\'umero de combinacines posibles con consonantes que sería: 106480000 combinaciones$ Mensaje modificado por Assassin.... el Nov 10 2007, 04:38 PM

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 7 2007, 08:21 AM Publicado: #10
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Ahora sí, todas las respuestas son correctas, aclarando que (en el ejercicio 1) existen 22 letras consonantes para las patentes Esperamos que el autor del problema entregue sus comentarios... -------------------- Sebastián Elías Puelma Moya Administrador FMAT

« Posterior · Problemas Resueltos · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 05:56 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.