Segundo Nivel Individual

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2007 > Cuarta Fecha

Segundo Nivel Individual, Santiago, Talagante, Rancagua

Opciones

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 16 2007, 09:15 PM Publicado: #1
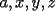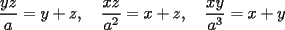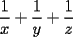Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Problema 1: Se sabe que los números positivos $TEX: $a, x, y, z$$ cumplen las siguientes igualdades $TEX: $\dfrac{yz}{a}=y+z, \quad\dfrac{xz}{a^2}=x+z, \quad\dfrac{xy}{a^3}=x+y$$ Encontrar en términos de $TEX: $a$$ , el valor de $TEX: $\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}$$ Problema 2: Consideremos las fichas de triminó como es indicado en las figuras, con caras 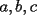$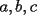TEX: $a, b, c$$ , donde las letras $TEX: $a, b, c$$ representan números naturales del conjunto $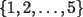TEX: $\{1, 2, \ldots, 5\}$$ . Vamos a considerar que dos fichas son iguales si una resulta de rotar la otra, o sea las siguientes tres fichas de triminó son la misma $TEX: \noindent $a)$$ ¿Cuántas fichas de triminó existen? $TEX: \noindent $b)$$ ¿Cuánto suman los números de todas las fichas de triminó? Indicación. Considere por separado los siguientes tres tipos de fichas de triminó: el primer tipo con todas sus caras iguales, el segundo tipo con dos caras iguales y la tercera cara distinta, y el tercer tipo con todas sus caras distintas. Como siempre están invitados a postear sus soluciones Saludos. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 21 2007, 07:35 PM Publicado: #2
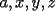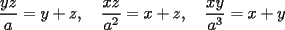Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Killua @ Aug 16 2007, 10:15 PM) Problema 1: Se sabe que los números positivos $TEX: $a, x, y, z$$ cumplen las siguientes igualdades $TEX: $\dfrac{yz}{a}=y+z, \quad\dfrac{xz}{a^2}=x+z, \quad\dfrac{xy}{a^3}=x+y$$ Encontrar en términos de $TEX: $a$$ , el valor de $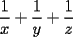TEX: $\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}$$ Solución al problema 1 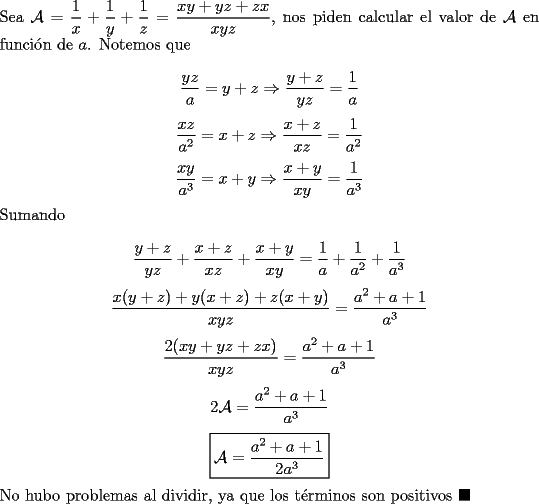$TEX: \noindent Sea $\mathcal{A}=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{xy+yz+zx}{xyz}$, nos piden calcular el valor de $\mathcal{A}$ en funci\'on de $a$. Notemos que<br /><br />$$\dfrac{yz}{a}=y+z\Rightarrow\dfrac{y+z}{yz}=\dfrac{1}{a}$$<br />$$\dfrac{xz}{a^2}=x+z\Rightarrow\dfrac{x+z}{xz}=\dfrac{1}{a^2}$$<br />$$\dfrac{xy}{a^3}=x+y\Rightarrow\dfrac{x+y}{xy}=\dfrac{1}{a^3}$$<br /><br />\noindent Sumando<br /><br />$$\dfrac{y+z}{yz}+\dfrac{x+z}{xz}+\dfrac{x+y}{xy}=\dfrac{1}{a}+\dfrac{1}{a^2}+\dfrac{1}{a^3}$$<br />$$\dfrac{x(y+z)+y(x+z)+z(x+y)}{xyz}=\dfrac{a^2+a+1}{a^3}$$<br />$$\dfrac{2(xy+yz+zx)}{xyz}=\dfrac{a^2+a+1}{a^3}$$<br />$$2\mathcal{A}=\dfrac{a^2+a+1}{a^3}$$<br />$$\boxed{\mathcal{A}=\dfrac{a^2+a+1}{2a^3}}$$<br /><br />\noindent No hubo problemas al dividir, ya que los t\'erminos son positivos $\blacksquare$$ Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

tioberlin Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 19 2011, 03:07 PM Publicado: #3
Matemático Grupo: Validating Mensajes: 50 Registrado: 22-October 11 Desde: Santiago Miembro Nº: 96.078 Nacionalidad: Colegio/Liceo: Sexo:	RP2: a)Las posibles combinaciones, por conveniencia, fueron ordenadas como numeros de 3 cifras, de menor a mayor, (111,112,113,114,115) (121,122.123.124.125). Notar que cada uno de estos paréntesis contiene 5 números, y que por cada centena (la del 100,200,300,400 y 500) habrán 5 de estos parentesis, y al haber 5 centenas, la respuesta es 5 elevado al cubo, 125 b)Una forma simple de resolver esta pregunta era ordenando los números de manera que el mayor numero quede con el menor, el segundo mayor con el segundo menor, hasta ocupar todos los numeros, es decir, (555+111) + (554+112) + (553+113) ... (332+334) + 333 Notemos que cada una de estas sumas da como resultado 666. Al ser 125 números, podemos crear 62 de estas sumas, y un numero quedara solo, que sera el 333, por lo tanto la respuesta es 62666 + 333 que da como resultado 41625*

« Posterior · Cuarta Fecha · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 11th April 2025 - 08:10 AM