|
|
|
|
|
|
|
  |
 Aug 7 2007, 03:01 PM Aug 7 2007, 03:01 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
Contruya la solución de
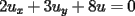 sujeto a sujeto a 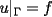 , con : , con :a) 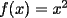 b) 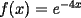 En ambos problemas, 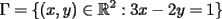 Saludos |
|
|
|
 Jul 2 2010, 12:48 AM Jul 2 2010, 12:48 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
![TEX: \noindent Usamos el método de las características con <br />\[\left(x(0,s),y(0,s),z(t,s)\right)=(\alpha(s),\beta(s),f(s))=\left(s,\frac{2s+1}{3},f(s)\right).\]<br />Luego, debemos resolver el sistema<br />\begin{eqnarray}<br />\dot x(t,s)=2\\<br />\dot y(t,s)=3\\<br />\dot z(t,s)=-8z(t,s)<br />\end{eqnarray}<br />de donde se obtiene que<br />\begin{eqnarray}<br />x(t,s)=2t+c_1(s)\\<br />y(t,s)=3t+c_2(s)\\<br />z(t,s)=c_3(s)e^{-8t}<br />\end{eqnarray}<br />Imponiendo las condiciones iniciales, tenemos que <br />\begin{eqnarray*}<br />x(0,s)=c_1(s)=s\\<br />y(0,s)=c_2(s)=\frac{2s+1}{3}\\<br />z(0,s)=c_3(s)=f(s)<br />\end{eqnarray*}<br />Luego,<br />\begin{enumerate}<br />\item[$a$)]$c_3(s)=s^2$<br />\item[$b$)]$c_3(s)=e^{-4s}$<br />\end{enumerate}<br />Finalmente, despejando, tenemos que<br />\[s=\frac{1}{5}\left(9x-6y+2\right)\quad , \quad t=-\frac{1}{5}\left(2x-3y+1\right),\]<br />es decir,<br />\begin{enumerate}<br />\item[$a$)]$u(x,t)=\frac{1}{25}\left(9x-6y+2\right)^2e^{\frac{1}{5}\left(2x-3y+1\right)}$.<br />\item[$b$)]$u(x,t)=e^{-\frac{4}{5}\left(9x-6y+2\right)}e^{\frac{1}{5}\left(2x-3y+1\right)}=e^{-\frac 15\left(38x-27y+9\right)}$.<br />\end{enumerate}<br />](./tex/ec8463402fb7b0e71e98649624732e55.png)
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 04:56 AM |











![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)

