|
|
|
|
|
|
|
  |
 Aug 4 2007, 09:02 PM Aug 4 2007, 09:02 PM
Publicado:
#1
|
|
 Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |

--------------------  Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat    "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados. |
|
|
|
 Aug 5 2007, 12:01 AM Aug 5 2007, 12:01 AM
Publicado:
#2
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 163 Registrado: 5-August 06 Desde: Concepción, Octava región. Miembro Nº: 1.853 Nacionalidad:  Colegio/Liceo:  Sexo:  |
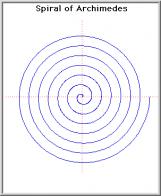
 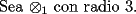 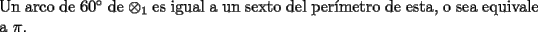 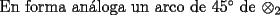 (de radio x) (de radio x)  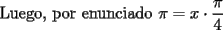  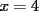 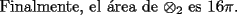
-------------------- "Me esfuerzo por ser mejor; y no él mejor" A.Flores
|
|
|
|
 Aug 5 2007, 03:19 PM Aug 5 2007, 03:19 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |

-------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"-
Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo.. |
|
|
|
 Aug 5 2007, 03:52 PM Aug 5 2007, 03:52 PM
Publicado:
#4
|
|
 Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
otra sol para el Problema 2
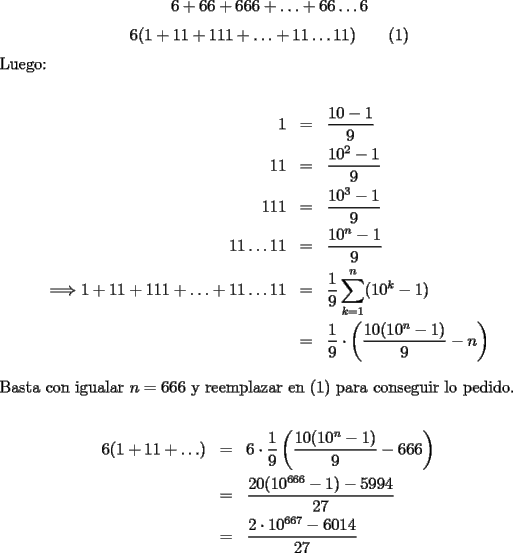
--------------------  Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat    "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados. |
|
|
|
| Cesarator |
 Sep 13 2007, 06:42 PM Sep 13 2007, 06:42 PM
Publicado:
#5
|
|
Invitado |
y el problema 3???
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 11th April 2025 - 08:16 AM |







