|
|
|
|
|
|
|
  |
 Jul 11 2007, 03:52 PM Jul 11 2007, 03:52 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |

-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Jul 12 2007, 02:04 AM Jul 12 2007, 02:04 AM
Publicado:
#2
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 19-July 06 Desde: Conce, Jazz Capitol Miembro Nº: 1.716 Nacionalidad:  Sexo:  |
Aquí va mi solución al 4. Me costó un mundo redactarla, asi que cualquier corrección es apreciada, pero creo que se entiende...

|
|
|
|
 Jul 12 2007, 09:50 PM Jul 12 2007, 09:50 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Aquí va mi solución al 4. Me costó un mundo redactarla, asi que cualquier corrección es apreciada, pero creo que se entiende...  Correcto, con eso basta... Error mio no decir que 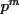 era entero, pero al postear este examen lo hice con lo que recordaba porque le pase la hoja a Kamelot despues del la prueba, luego, la redaccion no es la misma que en el original. era entero, pero al postear este examen lo hice con lo que recordaba porque le pase la hoja a Kamelot despues del la prueba, luego, la redaccion no es la misma que en el original.Saludos PD: Que bonito contar con ramos como este en la carrera... aunque me lo saque -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Aug 5 2007, 01:29 PM Aug 5 2007, 01:29 PM
Publicado:
#4
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 112 Registrado: 2-June 07 Miembro Nº: 6.357 |
Problema 2.-
Para el primer grupo serán las distintas agrupaciones formadas con 5 personas, eligiéndolos de entre los 15 Para el segundo, formadas con 5 personas, eligiendolas entre los 10 restantes. Finalmente el ultimo grupo queda creado con los restantes 5. Se divide por el total de permutaciones que hay entre los grupos 3! ![TEX: \[<br />\frac{{C_{15}^5 \cdot C_{10}^5 \cdot C_5^5 }}<br />{{3!}} = \frac{{\tfrac{{15!}}<br />{{5!10!}} \cdot \tfrac{{10!}}<br />{{5!5!}}}}<br />{{3!}}<br />\]](./tex/1186338548.gif)
-------------------- < romero jazmin flor de naranjo >
|
|
|
|
 Aug 5 2007, 01:36 PM Aug 5 2007, 01:36 PM
Publicado:
#5
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 112 Registrado: 2-June 07 Miembro Nº: 6.357 |
Problema 3.-
Para cada una de las 1001 personas pueden tener desde 0 a 1000 amigos. (en total 1001) Pero si hay una persona que tiene 0 amigos la máxima cantidad que puede tener otra persona es 999. (1000) Y si no hay persona que tenga 0 amigos, entonces el máximo puede ser 1000. (1000) Luego, de las 1001 personas, 1000 de ellas pueden tener una cantidad de amigos distintos, por lo que la persona sobrante tendrá que tener la misma cantidad que uno de esos 1000. -------------------- < romero jazmin flor de naranjo >
|
|
|
|
 Sep 3 2007, 02:52 PM Sep 3 2007, 02:52 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
|
|
|
|
 Feb 11 2008, 03:08 PM Feb 11 2008, 03:08 PM
Publicado:
#7
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 216 Registrado: 6-August 07 Desde: concepcion Miembro Nº: 8.270 Nacionalidad:  Universidad:  Sexo:  |
 -------------------- |
|
|
|
 Sep 17 2011, 10:39 PM Sep 17 2011, 10:39 PM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P2.-
Se tienen primero 15 alumnos y de ellos me interesa las formas de sacar 5 de ellos 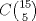 , luego teniendo en cuenta que ya saqué 5 alumnos, es , luego teniendo en cuenta que ya saqué 5 alumnos, es 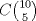 , de forma análoga ahora solo es , de forma análoga ahora solo es 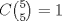 , como estos "eventos" deben ser simultáneos, entonces por principio multiplicativo se tendrá que el total de formas en que esto puede ocurrir es: , como estos "eventos" deben ser simultáneos, entonces por principio multiplicativo se tendrá que el total de formas en que esto puede ocurrir es: 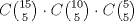 . .No es necesario dividir por la permutación de estos 3 grupos, pues preguntan en cuantas formas se pueden dividir, no en cuantas formas se puede ordenar estos 3 grupos Saludos! PD: me llamó la atención el nombre de este subforo, bacán un ramo así -------------------- Me voy, me jui.
|
|
|
|
 Sep 18 2011, 01:25 PM Sep 18 2011, 01:25 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
-------------------- |
|
|
|
 May 26 2012, 01:44 AM May 26 2012, 01:44 AM
Publicado:
#10
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 80 Registrado: 10-May 07 Desde: Chillán Miembro Nº: 5.752 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Tengo una demostración para el P3:
Por contradicción, supongamos que es falso que al menos dos personas tienen la misma cantidad de amigos dentro de la sala; luego supongamos que ninguna persona tiene la misma cantidad de amigos dentro de la sala. Luego es evidente que a lo mas una persona en la sala puede tener 1000 amigos; ya que no peude ser amigo de si mismo. Y a lo menos puede tener 0 amigos. luego las cantidades de amigos 0,1,2,3,4,....1000; estarian repartidas para cada uno de las personas. Esto satisface la suposición de que cada persona tenga una cantidad diferente de amigos en la sala. Pero ahora notemos que la persona con 1000 amigos si o si es amigo de todos los demas en la sala; eso incluye a la persona que tiene 0 amigos, Esto nos lleva a una contradicción. Y por ende queda demostrado. Bueno ojala opinen que onda, pa cachar si esta bien esta demostración o esta muy flaite,jaja. Saludos chau!! Mensaje modificado por lipexx el May 26 2012, 01:53 AM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 10:03 PM |











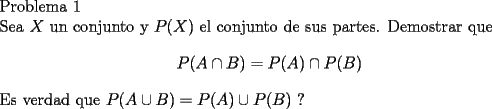
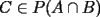 . Luego
. Luego 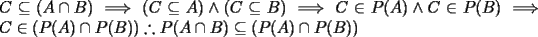
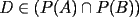
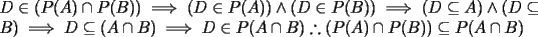
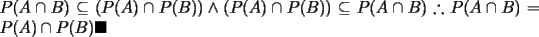
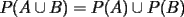 , basta darse un contraejemplo sencillo, tomemos
, basta darse un contraejemplo sencillo, tomemos 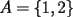 y
y 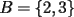 . Claramente
. Claramente 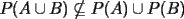 pues
pues 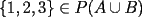 , sin embargo
, sin embargo 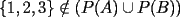 , luego, la igualdad no se verifica.
, luego, la igualdad no se verifica.

