|
|
|
|
|
|
|
  |
 Jul 7 2007, 04:17 PM Jul 7 2007, 04:17 PM
Publicado:
#1
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 122 Registrado: 6-October 06 Desde: VIII Región Miembro Nº: 2.438 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 ![TEX: <br />\[<br />\begin{array}{l}<br /> {\rm Sea\ }p_n {\rm\ la\ sucesion\ de\ los\ numeros\ primos}{\rm\ . Es\ decir\ }{\rm ,\ }p_1 = 2,p_2 = 3,{\rm }p_3 = 5, \\ <br /> p_4 = 7,{\rm }p_5 = 11,....{\rm Demostrar\ que\ para\ todo\ }k \in {\rm N},{\rm }k \ge 2,{\rm se\ tiene\ que\ } \\ <br /> {\rm }p_{k + 1} < {\rm }p_1 \cdotp_2 {\rm \cdot}p_3 {\rm \cdot}.......{\rm \cdot}p_k {\rm } \\ <br /> \end{array}<br />\]<br />](./tex/1183843071.gif)  ![TEX: <br />\[<br />\begin{array}{l}<br /> {\rm Encontrar\ todos\ los\ numeros\ enteros\ }a,b{\rm\ tales\ que} \\ <br /> {\rm }a^2 = b^4 + 19 \\ <br /> \end{array}<br />\]<br />](./tex/1183843074.gif)  ![TEX: <br />\[<br />\begin{array}{l}<br /> {\rm Dado\ un\ numero\ entero\ positivo}{\rm , definimos\ su\ coeficiente\ }S_9 {\rm\ como\ la\ } \\ <br /> {\rm suma\ de\ las\ potencias\ novenas\ de\ sus\ digitos}{\rm .\ Asi}{\rm , por\ ejemplo}{\rm ,} \\ <br /> {\rm }S_9 (47) = 4^9 + 7^9 ,{\rm }S_9 (11509) = 1^9 + 1^9 + 5^9 + 0^9 + 9^9 \\ <br /> {\rm Considerar\ el\ conjunto\ de\ los\ enteros\ de\ 10\ o\ menos\ digitos:} \\ <br /> {\rm }K = \{ 1,2,3,.....,9999999998,9999999999\} \\ <br /> {\rm Demostrar\ que\ si\ }n \in K,{\rm entonces\ }S_9 (n) \in K \\ <br /> \end{array}<br />\]<br />](./tex/1183843078.gif)
|
|
|
|
 Jul 7 2007, 10:32 PM Jul 7 2007, 10:32 PM
Publicado:
#2
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 122 Registrado: 6-October 06 Desde: VIII Región Miembro Nº: 2.438 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 ![TEX: <br />\[<br />\begin{array}{l}<br /> a^2 = b^4 + 19 \\ <br /> a^2 - b^4 = 19 \\ <br /> (a + b^2 )(a - b^2 ) = 19 \\ <br /> \end{array}<br />\]<br />](./tex/1183865784.gif)  ![TEX: <br />1<br />\[<br />\begin{array}{l}<br /> a + b^2 = 1 \\ <br /> a - b^2 = 19 \\ <br /> a = 19 + b^2 \\ <br /> 19 + b^2 + b^2 = 1 \\ <br /> 2b^2 = - 18 \\ <br /> b^2 = - 9 \\ <br /> b = - 3 \\ <br /> a = 10 \\ <br /> \end{array}<br />\]<br />](./tex/1183865787.gif) ![TEX: <br />2<br />\[<br />\begin{array}{l}<br /> a + b^2 = - 1 \\ <br /> a - b^2 = - 19 \\ <br /> a = - 19 + b^2 \\ <br /> - 19 + b^2 + b^2 = - 1 \\ <br /> 2b^2 = 18 \\ <br /> b^2 = 9 \\ <br /> b = 3 \\ <br /> a = - 10 \\ <br /> \end{array}<br />\]<br />](./tex/1183865790.gif) ![TEX: <br />3<br />\[<br />\begin{array}{l}<br /> a + b^2 = 19 \\ <br /> a - b^2 = 1 \\ <br /> a = 1 + b^2 \\ <br /> 1 + b^2 + b^2 = 19 \\ <br /> 2b^2 = 18 \\ <br /> b^2 = 9 \\ <br /> b = 3 \\ <br /> a = 10 \\ <br /> \end{array}<br />\]<br />](./tex/1183865793.gif) ![TEX: <br />4<br />\[<br />\begin{array}{l}<br /> a + b^2 = - 19 \\ <br /> a - b^2 = - 1 \\ <br /> a = - 1 + b^2 \\ <br /> - 1 + b^2 + b^2 = - 19 \\ <br /> 2b^2 = - 18 \\ <br /> b^2 = - 9 \\ <br /> b = - 3 \\ <br /> a = - 10 \\ <br /> \end{array}<br />\]<br />](./tex/1183865994.gif) 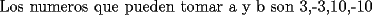
Mensaje modificado por Nilrem el Jul 7 2007, 10:39 PM |
|
|
|
 Jul 18 2007, 11:47 AM Jul 18 2007, 11:47 AM
Publicado:
#3
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 329 Registrado: 24-August 06 Desde: Concepción Miembro Nº: 2.038 Nacionalidad:  Colegio/Liceo:  Sexo:  |
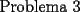 ![TEX: <br />\[<br />\begin{array}{l}<br /> {\rm Dado\ un\ numero\ entero\ positivo}{\rm , definimos\ su\ coeficiente\ }S_9 {\rm\ como\ la\ } \\ <br /> {\rm suma\ de\ las\ potencias\ novenas\ de\ sus\ digitos}{\rm .\ Asi}{\rm , por\ ejemplo}{\rm ,} \\ <br /> {\rm }S_9 (47) = 4^9 + 7^9 ,{\rm }S_9 (11509) = 1^9 + 1^9 + 5^9 + 0^9 + 9^9 \\ <br /> {\rm Considerar\ el\ conjunto\ de\ los\ enteros\ de\ 10\ o\ menos\ digitos:} \\ <br /> {\rm }K = \{ 1,2,3,.....,9999999998,9999999999\} \\ <br /> {\rm Demostrar\ que\ si\ }n \in K,{\rm entonces\ }S_9 (n) \in K \\ <br /> \end{array}<br />\]<br />](./tex/1183843078.gif) Busquemos el menor S9 posible. Claramente es el de 1 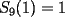 Pertenece a K Y el mayor S9 posible es obviamente el de 999999999 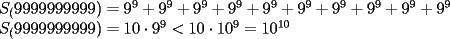 Vemos que al ser menor que 10^10, el S9 de 9999999999 tiene 10 o menos dígitos y por tanto pertenece a K. Ya que todos los S9 de los N°s del conjunto K se mueven entre los dos anteriores, podemos asegurar que lo pedido en el enunciado es cierto. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 11th April 2025 - 08:09 AM |









