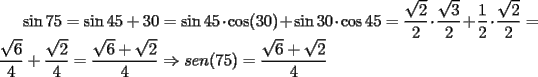Examen 2007 - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Geometría

Examen 2007, Lic. en Matemática

Opciones

Pily Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 1 2007, 05:30 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: 1. (a)Si el lado del dodec\' agono (12 lados) regular mide 2 cm., demuestre que el radio de la correspondiente circunferencia circunscrita mide, exactamente, $\sqrt{6}+\sqrt{2}$ cm. \\<br />$ $ \\<br />(b) Sean A( $\vec{a}$ ), B( $\vec{b}$ ), C( $\vec{c}$ ), tres puntos del espacio, no colineales. Demuestre que el vector: $\vec{a}$ x $\vec{b}+\vec{b}$ x $\vec{c}+\vec{c}$ x $\vec{a}$ es paralelo al vector normal al plano determinado por los tres puntos. ¿Qu\' e f\' ormula vectorial se deduce si los tres puntos son colineales? \\<br />$ $ \\<br />2. (a) Dos lados de un cuadrado tienen por ecuaci\' on: $4x+3y+3=0$, $4x+3y-17=0$, respectivamente y uno de sus v\' ertices es el punto $(2,3)$. Determine la ecuaci\' on de los otros dos lados de este cuadrado (dos soluciones).\\<br />$ $ \\<br />(b) Demuestre que las rectas de ecuaciones: {$3x-2y-2z+1=0$, $6x+2y-z-7=0$}, $\dfrac{x+1}{2}=\dfrac{y+2}{-3}=\dfrac{z-13}{6}$ son paralelas, determine la ecuaci\' on del plano que las contiene y calcule la distancia entre ellas. \\<br />$ $ \\<br />3. (a) El centro C de la circunferencia $c$ de ecuaci\' on: $x^2+y^2-2kx-2y-6=0$ (siendo k un entero) forma con el foco A de la par\' abola de ecuaci\' on: $y^2-8x-6y+1=0$, y con el centro B de la elipse de ecuaci\' on: $9x^2+16y^2-36x+128y+88=0$ un tri\' angulo ABC de \' area igual a 6. Cu\' anto mide el \' area del c\' irculo encerrado por $c$?<br />$ $ \\<br />(b) Dada la par\' abola P de ecuaci\' on: $y^2=12x$, y la recta $l$ de ecuaci\' on: $3x-y-5=0$, determine la ecuaci\' on del di\' ametro $dm$ que dimidia a la cuerda formada por P y $l$. Luego determine la ecuaci\' on de la recta tangente a P en el punto donde ella es cortada por $dm$.<br />$ $ \\<br />$ $ \\<br />4. (a) Demuestre que el punto del plano correspondiente al complejo $(1+i)^{1305}$ pertenece a la curva (conocida como espiral logaritmica) de ecuaci\' on polar: $\rho = 4^{\frac{\theta }{\pi }} $.<br />$ $ \\<br />$ $ \\<br />(b) Los puntos A y B del plano corresponden a los complejos que son ra\' ices de la ecuaci\' on: $z^2-2(2+3i)z-2(1-4i)=0$. Determine las coordenadas del punto C tal que el tri\' angulo ABC es equil\' atero (dos soluciones).$ --------------------

Pily Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 4 2007, 01:29 PM Publicado: #2
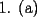Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad: Colegio/Liceo: Sexo:	La más facilita: $TEX: 1. (a)$ Previo: $TEX: $\sin{75}=\sin{45+30}=\sin{45}\cdot \cos(30)+\sin{30}\cdot \cos{45}=\dfrac{\sqrt{2}}{2}\cdot \dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\cdot \dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{4}=\dfrac{\sqrt{6}+\sqrt{2}}{4}\Rightarrow sen(75)=\dfrac{\sqrt{6}+\sqrt{2}}{4}$$ Consideremos la figura, sean C el centro de la circunferencia y R el radio de ella. Notemos primero que 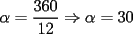$TEX: $\alpha = \dfrac{360}{12} \Rightarrow \alpha = 30$$ . 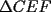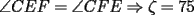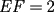Siendo $TEX: $\Delta CEF$$ isósceles, tenemos que $TEX: $\angle CEF = \angle CFE \Rightarrow \zeta = 75$$ Además $TEX: $EF=2$$ , y por Teo. 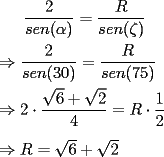del Seno tendremos: $TEX: $\dfrac{2}{sen(\alpha )}=\dfrac{R}{sen(\zeta )}$ \\<br />$ $ \\<br />$ \Rightarrow \dfrac{2}{sen(30)}=\dfrac{R}{sen(75)}$ \\<br />$ $ \\<br />$\Rightarrow 2\cdot \dfrac{\sqrt{6}+\sqrt{2}}{4} = R\cdot \dfrac{1}{2}$ \\<br />$ $ \\<br />$\Rightarrow R = \sqrt{6} + \sqrt{2}$$ --------------------

« Posterior · Geometría · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 10th April 2025 - 11:52 AM