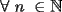|
|
|
|
|
|
|
  |
 Jun 27 2007, 09:53 PM Jun 27 2007, 09:53 PM
Publicado:
#1
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Para mí, no estuvo tan difícil como esperaba.
![TEX: $ $ \\<br />$\text{MAT1115 Examen}$ \\<br />$ $ \\<br />1. (a) Calcule la suma de $2n$ t\' erminos \\<br />$$1^2 - 2^2+3^2-4^2\dots $$ \\<br />(b) Demuestre el resultado de la parte (a) usando inducci\' on matematica. \\<br />$ $ \\<br />2. (a) Encuentre el punto de intersecci\' on de las rectas tangentes a la curva $y=x^2$ en los puntos $(x_0,y_0)$, $(-x_0,y_0)$. \\<br />(b) Determinar el valor m\' aximo y m\' inimo del polinomio \\<br />$$y=2x^3-3x^2-12x$$ \\<br />en el intervalo [0,3]. \\<br />$ $ \\<br />3. Sea $f(x)=2\sqrt{x^2+5x+6}-\sqrt{x^2-2x+5}$. Determine el dominio de $f$ y calcule $\displaystyle\lim_{x\to -\infty}\dfrac{f(x)}{x}$ \\<br />$ $ \\<br />$ $ \\<br />4. Calcule la derivada de las siguientes funciones: \\<br />(a) $f(x)=\cos (3\sin (x)-2\cos ^2(x)+\sqrt{x^2+x+1})$ \\<br />(b) $f(x)=arctan(\sin ^2(3x+2)-3\cos (5x))$ \\<br />(No es necesario que simplifique sus resultados) \\<br />$ $ \\<br />5. (a) Enuncie el Teorema del Valor Intermedio \\<br />(b) Enuncie el Teorema del Valor Medio \\<br />© Enuncie el Teorema de Taylor.](./tex/1182999202.gif)
--------------------  |
|
|
|
 Jun 28 2007, 12:21 PM Jun 28 2007, 12:21 PM
Publicado:
#2
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 121 Registrado: 6-December 05 Desde: Las Condes - Chillán Miembro Nº: 460 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Pily te pasaste!!!
Aunque no tengo el mismo calculo me servira para estudiar Gracias!!!!!!!!! |
|
|
|
 Jun 28 2007, 01:46 PM Jun 28 2007, 01:46 PM
Publicado:
#3
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Pily te pasaste!!! Aunque no tengo el mismo calculo me servira para estudiar Gracias!!!!!!!!! [jugo] En too caso xD, los Maples (para nosotros) eran bien raros, casi na' que ver con lo que estábamos viendo xD[/jugo] La idea igual es que se vaya resolviendo, así se aclaran las dudas que se puedan tener. Igual no estaba difícil. Parto yo con el 1: Mensaje modificado por Pily el Jan 6 2008, 01:35 PM --------------------  |
|
|
|
 Jun 28 2007, 06:30 PM Jun 28 2007, 06:30 PM
Publicado:
#4
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 24 Registrado: 14-June 05 Desde: Aquí... Miembro Nº: 106 Nacionalidad:  Sexo:  |
Wuaaa ellaaaa.. la diosa del taylor xD
Igual la usaré para estudiar! tengo prueba la otra semana y control por la mañanita xD Gracias por tu aporte Filar. Celebraremos apenas pase Quimica. =) Bye --------------------  |
|
|
|
 Jun 29 2007, 01:58 PM Jun 29 2007, 01:58 PM
Publicado:
#5
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 121 Registrado: 6-December 05 Desde: Las Condes - Chillán Miembro Nº: 460 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |

|
|
|
|
 Jul 1 2007, 04:47 PM Jul 1 2007, 04:47 PM
Publicado:
#6
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad:  Colegio/Liceo:  Sexo:  |
![TEX: \[<br />\begin{gathered}<br /> {\text{Primero derivamos el polinomio:}} \hfill \\<br /> y = 2x^3 - 3x^2 - 12x \Rightarrow y' = 6x^2 - 6x - 12 = 6(x^2 - x - 2) \Rightarrow y' = 6(x + 1)(x - 2) \hfill \\ <br />\end{gathered} <br />\]](./tex/1183326462.gif) Recordemos que los candidatos a máximos y mínimos son los puntos en los que 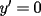 , cuando y' se indetermina y/o los extremos del intervalo. Por lo tanto , cuando y' se indetermina y/o los extremos del intervalo. Por lo tanto![TEX: \[<br />\begin{gathered}<br /> (i){\text{ }}y' = 0 \Leftrightarrow x = 2 \vee x = - 1 \hfill \\<br /> (ii){\text{ No hay punto de indefinici\'o n de }}y' \hfill \\<br /> (iii){\text{ Extremos del intervalo: }}x = 0,{\text{ }}x = 3 \hfill \\<br /> \hfill \\<br /> {\text{Pero }} - 1 \notin [0,3],{\text{ luego evaluamos el polinomio s\'o lo en }}x = 2,x = 0,{\text{ }}x = 3: \hfill \\<br /> y(0) = 0 \hfill \\<br /> y(2) = 16 - 12 - 24 = - 20 \hfill \\<br /> y(3) = 54 - 27 - 36 = - 9 \hfill \\ <br />\end{gathered} <br />\]](./tex/1183326467.gif) De esto se concluye que el valor mínimo se alcanza en 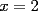 y es y es 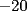 , mientras que el valor máximo se alcanza en , mientras que el valor máximo se alcanza en 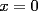 y es y es  . .
--------------------  |
|
|
|
 Jul 6 2007, 09:48 PM Jul 6 2007, 09:48 PM
Publicado:
#7
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 72 Registrado: 28-April 07 Miembro Nº: 5.504 Nacionalidad:  Universidad:  Sexo:  |
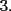 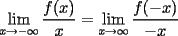 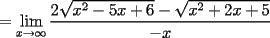 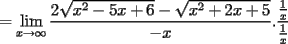 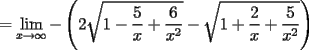 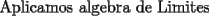 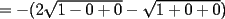 
Mensaje modificado por beethoven el Jul 6 2007, 09:53 PM |
|
|
|
 Jul 6 2007, 10:19 PM Jul 6 2007, 10:19 PM
Publicado:
#8
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 72 Registrado: 28-April 07 Miembro Nº: 5.504 Nacionalidad:  Universidad:  Sexo:  |
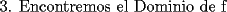  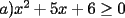 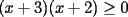 ![TEX: $a>0 \Longrightarrow x \in (-\infty ,-3]\bigcup [-2,+\infty )$](./tex/1183832302.gif) 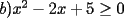 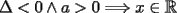 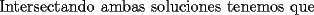 ![TEX: $\text{Dom}(f)=(-\infty ,-3]\bigcup [-2,+\infty )$](./tex/1183832309.gif)
Mensaje modificado por beethoven el Jul 7 2007, 01:18 PM |
|
|
|
 Jul 7 2007, 01:34 PM Jul 7 2007, 01:34 PM
Publicado:
#9
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 72 Registrado: 28-April 07 Miembro Nº: 5.504 Nacionalidad:  Universidad:  Sexo:  |
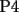 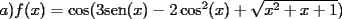 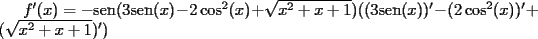 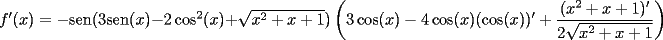 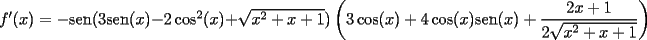 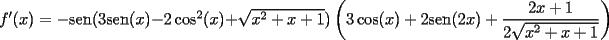
Mensaje modificado por beethoven el Jul 7 2007, 01:45 PM |
|
|
|
 Jul 7 2007, 02:04 PM Jul 7 2007, 02:04 PM
Publicado:
#10
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 72 Registrado: 28-April 07 Miembro Nº: 5.504 Nacionalidad:  Universidad:  Sexo:  |
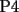 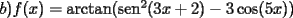 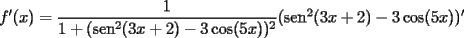 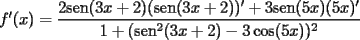 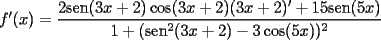 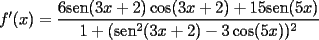
|
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 26th April 2025 - 01:02 PM |










![TEX: \[<br />\begin{gathered}<br /> 1^2 + 3^2 + 5^2 \ldots - (2^2 + 4^2 + 6^2 \ldots ) \hfill \\<br /> \Rightarrow \sum\limits_{k = 1}^{n} {(2k - 1)^2 } - \sum\limits_{k = 1}^{n} {(2k)^2 } \hfill \\<br /> \Rightarrow 4\sum\limits_{k = 1}^{n} {k^2 } - 4\sum\limits_{k = 1}^{n} {k + \sum\limits_{k = 1}^{n} 1 } - 4\sum\limits_{k = 1}^{n} {k^2 } \hfill \\<br /> \Rightarrow - 4\sum\limits_{k = 1}^{n} {k + \sum\limits_{k = 1}^{n} 1 } \hfill \\<br /> \Rightarrow n - \frac{{4\cdot n(n + 1)}}<br />{2} \hfill \\<br /> \Rightarrow n - 2n(n + 1) \hfill \\<br /> \Rightarrow n - 2n^2 - 2n \hfill \\<br /> \Rightarrow - 2n^2 - n \hfill \\<br />\end{gathered}<br />\]<br />](./tex/145cbb0847146673dd1e14082190e0e4.png)
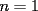 :
:![TEX: \[<br /> \Rightarrow \sum\limits_{k = 1}^2 {(2k - 1)^2 } - \sum\limits_{k = 1}^2 {(2k)^2 } = 1^2 + 3^2 - \left( {2^2 + 4^2 } \right) = 10 - 20 = - 10<br />\]](./tex/1183056422.gif)
![TEX: \[<br />- 8 \cdot (1)^2 - 2 \cdot 1 = - 10<br />\]](./tex/1183056424.gif)
![TEX: \[<br />\sum\limits_{k = 1}^{2n} {(2k - 1)^2 } - \sum\limits_{k = 1}^{2n} {(2k)^2 } = - 8n^2 - 2 \cdot n<br />\]](./tex/1183683752.gif) ,
, ![TEX: \[<br />\forall n \in \mathbb{N}<br />\]](./tex/1183056427.gif)
![TEX: \[<br />\sum\limits_{k = 1}^{2(n + 1)} {(2k - 1)^2 } - \sum\limits_{k = 1}^{2(n + 1)} {(2k)^2 } = - 8(n + 1)^2 - 2(n + 1)<br />\]](./tex/1183056429.gif)
![TEX: \[<br />\begin{gathered}<br /> \Rightarrow \sum\limits_{k = 1}^{2n + 2} {(2k - 1)^2 } - \sum\limits_{k = 1}^{2n + 2} {(2k)^2 } = - 8(n + 1)^2 - 2(n + 1) \hfill \\<br /> \Rightarrow \sum\limits_{k = 1}^{2n} {(2k - 1)^2 } + (2(2n + 1) - 1)^2 + (2(2n + 2) - 1)^2 - \left( {\sum\limits_{k = 1}^{2n} {(2k)^2 } + (2(2n + 1))^2 + (2(2n + 2))^2 } \right){\text{ }} \hfill \\<br /> \Rightarrow \sum\limits_{k = 1}^{2n} {(2k - 1)^2 } + (4n + 1)^2 + (4n + 3)^2 - \left( {\sum\limits_{k = 1}^{2n} {(2k)^2 } + (4n + 2)^2 + (4n + 4)^2 } \right) \hfill \\<br /> \Rightarrow \underbrace {\sum\limits_{k = 1}^{2n} {(2k - 1)^2 } - \sum\limits_{k = 1}^{2n} {(2k)^2 } }_{ - 8n^2 - 2n} + (4n + 1)^2 + (4n + 3)^2 - (4n + 2)^2 - (4n + 4)^2 \hfill \\<br /> \hfill \\<br /> \Rightarrow - 8n^2 - 2n + 8n + 1 + 24n + 9 - 16n - 4 - 32n - 16 \hfill \\<br /> \Rightarrow - 8n^2 - 18n - 10 \hfill \\<br /> \Rightarrow - 8n^2 - 16n - 8 - 2n - 2 \hfill \\<br /> \Rightarrow - 8(n^2 + 2n + 1) - 2(n + 1) \hfill \\<br /> \Rightarrow - 8(n + 1)^2 - 2(n + 1) \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/1183056432.gif)