Prueba Final, Nivel mayor, 2010 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Olimpiadas > Olimpiada Nacional

5 Páginas:

< 1 2 3 4 > »

Reply to this topic

Start new topic

Prueba Final, Nivel mayor, 2010

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 08:15 PM Publicado: #11
Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(EnemyOfGod286 @ Oct 21 2010, 09:08 PM) Primer problema de geometría decente que veo en la nacional No estoy de acuerdo, sólo mira los p6 de la nacional 2006 y 2007 =) Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 08:24 PM Publicado: #12
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	CITA(Killua @ Oct 21 2010, 09:15 PM) No estoy de acuerdo, sólo mira los p6 de la nacional 2006 y 2007 =) Saludos que mire le probelma de la fórmula de Humbertito -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 08:39 PM Publicado: #13
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Sin contar el problema de geometría la prueba estuvo bastante accesible, supongo que los chicos del IN hicieron el 1 porque hicmos unos muy parecido por no decir igual hace un tiempo ¬¬ saludos y suerte para mañana P1) Denotemos $TEX: $x=a-b$$ , reemplazando en la ecuación tenemos que $TEX: $0=3(a-x)^2-x-2a^2=a^2-6ax-3x^2-x$ <br />$ Que es una ecuación cuadrática que tiene por discriminante un cuadrado perfecto pues tiene soluciones enteras $TEX: $·=48x^2+4x=4x(12x+1)$$ Como $TEX: $(x,12x+1)=1$$ se concluye que $TEX: $x=a-b$$ es un cuadrado perfecto. La otra es lo mismo poniendo $TEX: $x=a+b$$ -------------------- blep

xD13G0x Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 08:56 PM Publicado: #14
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad: Sexo:	Solucoin problema 1: $TEX: $2a^2+a^2=3b^2+b\Leftrightarrow (a-b)(2a+2b+1)=b^2$$ Suponga lo contrario, que $TEX: $a-b$$ no es cuadrado perfecto. Entonces existe un primo $TEX: $p$$ tal que $TEX: $p^{2k+1}\|a-b$$ pero $TEX: $p^{2k+2}\nmid a-b$$ para cierto entero no negativo $TEX: $k$$ . Tenemos que $TEX: $p^{2k+1}\|b^2\Rightarrow p^{k+1}\|b\Rightarrow b=p^{k+1}d$$ para cierta $TEX: $d$$ . Tenemos que $TEX: $p^{2k+1}\|a-b=a-p^{k+1}d\Rightarrow p^{k+1}\|a\Rightarrow a=p^{k+1}c$$ para cierto $TEX: $c$$ . La ecuacion se nos transforma en $TEX: $p^{k+1}(c-d)(2p^{k+1}(c+d)+1)=(p^{k+1}d)^2\Rightarrow (c-d)(2p^{k+1}(c+d)+1)=p^{k+1}d^2$$ pero tenemos que $TEX: $2p^{k+1}(c+d)+1$$ es coprimo con $TEX: $p$$ asi que $TEX: $p^{k+1}\|c-d\Rightarrow p^{2k+2}\|p^{k+1}(c-d)=a-b$$ contradiccion. Entonces $TEX: $a-b$$ es cuadrado perfecto y por lo tanto $TEX: $2a+2b+1$$ tambien. PD: lo otro es la misma *** xd -------------------- "I've never let my school interfere with my education.”

Emi_C Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 09:07 PM Publicado: #15
Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 5-April 10 Desde: Arg Miembro Nº: 67.793 Nacionalidad: Sexo:	CITA(xD13G0x @ Oct 21 2010, 09:56 PM) Solucoin problema 1: $TEX: $2a^2+a^2=3b^2+b\Leftrightarrow (a-b)(2a+2b+1)=b^2$$ Suponga lo contrario, que $TEX: $a-b$$ no es cuadrado perfecto. Entonces existe un primo $TEX: $p$$ tal que $TEX: $p^{2k+1}\|a-b$$ pero $TEX: $p^{2k+2}\nmid a-b$$ para cierto entero no negativo $TEX: $k$$ . Tenemos que $TEX: $p^{2k+1}\|b^2\Rightarrow p^{k+1}\|b\Rightarrow b=p^{k+1}d$$ para cierta $TEX: $d$$ . Tenemos que $TEX: $p^{2k+1}\|a-b=a-p^{k+1}d\Rightarrow p^{k+1}\|a\Rightarrow a=p^{k+1}c$$ para cierto $TEX: $c$$ . La ecuacion se nos transforma en $TEX: $p^{k+1}(c-d)(2p^{k+1}(c+d)+1)=(p^{k+1}d)^2\Rightarrow (c-d)(2p^{k+1}(c+d)+1)=p^{k+1}d^2$$ pero tenemos que $TEX: $2p^{k+1}(c+d)+1$$ es coprimo con $TEX: $p$$ asi que $TEX: $p^{k+1}\|c-d\Rightarrow p^{2k+2}\|p^{k+1}(c-d)=a-b$$ contradiccion. Entonces $TEX: $a-b$$ es cuadrado perfecto y por lo tanto $TEX: $2a+2b+1$$ tambien. PD: lo otro es la misma *** xd Mi solucion es un webiando un poco mas, pero a nuestro amigo le dio un apuro x colocar su solucion cuando le dije q ya lo resolvi 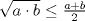. -------------------- $TEX: $\sqrt{a \cdot b} \le \frac{a+b}{2}$$

Robertinhox_xD Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 09:09 PM Publicado: #16
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 29 Registrado: 29-June 08 Desde: Santiago Centro Miembro Nº: 28.578 Nacionalidad: Colegio/Liceo: Sexo:	CITA(EnemyOfGod286 @ Oct 21 2010, 08:08 PM) Primer problema de geometría decente que veo en la nacional y pa que taaaan superiooor supremee ... xDDDDDDDDDDDD --------------------

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 09:49 PM Publicado: #17
Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Hints para una solución alternativa al p3: Si M es el punto medio de BC, N el de AX. 1. Trazar una perpendicular a BC por X, que corte a MN en I (punto que queremos probar es el incentro). El problema es equivalente a probar que XI=r, con r el inradio de ABC. ¿Cómo? Recordar que A=sr. 2. Trazar la altura h_a y una perpendicular de N a BC. Notar la razón entre estas alturas. 3. Si b = angulo(NMX), encontrar una expresión para tg(b) en el triángulo IXM. Usar teorema del coseno en cierto ángulo conveniente. Al final, les va quedar que XI = A/s. Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Nabodorbuco Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 22 2010, 06:16 AM Publicado: #18
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 513 Registrado: 25-April 08 Desde: CSMC Miembro Nº: 21.189 Nacionalidad: Colegio/Liceo: Sexo:	Era necesario aplicar induccion en el P2 ???? -------------------- FunGeometry SIEMPRE CON LAS MEJORES INTENCIONES DE AYUDAR. ATTE. NABODORBUCO EL TERCER OJO GoGeometry LA IDEA ES QUE NO ESPERES QUE FMAT RESUELVA TUS TAREAS, ESCRIBE SIEMPRE CUALES SON TUS INQUIETUDES

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 22 2010, 08:43 AM Publicado: #19
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Nabodorbuco @ Oct 22 2010, 08:16 AM) Era necesario aplicar induccion en el P2 ???? Nop, de hecho es cosa de separar el factorial.. $TEX: $10^{10}!=1\cdot 2\cdot \dots \cdot 10^{10}$$ el otro número es $TEX: $10^{10}$$ veces $TEX: $10^{10}$$ ahi altiro se tiene la desigualdad saludos :B -------------------- blep

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 22 2010, 11:49 AM Publicado: #20
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(snw @ Oct 22 2010, 08:43 AM) Nop, de hecho es cosa de separar el factorial.. $TEX: $10^{10}!=1\cdot 2\cdot \dots \cdot 10^{10}$$ el otro número es $TEX: $10^{10}$$ veces $TEX: $10^{10}$$ ahi altiro se tiene la desigualdad saludos :B No se si estaré muleando, pero ese ejercicio me parece como obvio mira: $TEX: $ $\\<br />$10^{10^{10^{10}}}>(10^{10})^{(10^{10})}$ y como $n^{n}\geq n!$ estamos listos no?$ Mensaje modificado por Kaissa el Oct 22 2010, 11:49 AM -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

« Posterior · Olimpiada Nacional · Anterior »

5 Páginas:

< 1 2 3 4 > »

Reply to this topic

Start new topic

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 30th April 2025 - 07:55 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.