|
|
|
|
|
|
|
  |
 Apr 16 2008, 05:52 PM Apr 16 2008, 05:52 PM
Publicado:
#1
|
|
 Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
tengo que encontrar todos lo valores de x en los reales, tales que
![TEX: \[<br />\left| x \right| < x^2 <br />\]<br />](./tex/dcd5f2fe9d5dc9071dffe62301fa1493.png) esto hice: ![TEX: \[<br />\begin{gathered}<br /> \left| x \right| < x^2 /()^2 \hfill \\<br /> x^2 < x^4 / \cdot \frac{1}<br />{{x^2 }} \hfill \\<br /> 1 < x^2 /\sqrt {} \hfill \\<br /> 1 < \left| x \right| \hfill \\<br /> - 1 < x < 1 \hfill \\<br /> \hfill \\<br /> S = \left( { - 1,1} \right) \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/81afa5b54eda6d88c2e06b2cb00d7527.png) pero lo logico, es todo al reves xD, es decir todos los reales menos S, que hice mal? -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico  “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti ![TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />](/tex-image/662cf378c88b8d7170f7919ce7dc427a.png) |
|
|
|
 Apr 16 2008, 06:03 PM Apr 16 2008, 06:03 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
tengo que encontrar todos lo valores de x en los reales, tales que ![TEX: \[<br />\left| x \right| < x^2 <br />\]<br />](./tex/dcd5f2fe9d5dc9071dffe62301fa1493.png) esto hice: ![TEX: \[<br />\begin{gathered}<br /> \left| x \right| < x^2 /()^2 \hfill \\<br /> x^2 < x^4 / \cdot \frac{1}<br />{{x^2 }} \hfill \\<br /> 1 < x^2 /\sqrt {} \hfill \\<br /> 1 < \left| x \right| \hfill \\<br /> - 1 < x < 1 \hfill \\<br /> \hfill \\<br /> S = \left( { - 1,1} \right) \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/81afa5b54eda6d88c2e06b2cb00d7527.png) pero lo logico, es todo al reves xD, es decir todos los reales menos S, que hice mal? Lo que tienes que tener claro es que 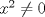 ya que si no estarías dividiendo por cero, luego lo correcto es extraer raíz, "no'' multiplicar por raíz, ya que multiplicar por el operador raíz no tiene sentido, al parecer se ve bien considerando las restricciones. Saludos. ya que si no estarías dividiendo por cero, luego lo correcto es extraer raíz, "no'' multiplicar por raíz, ya que multiplicar por el operador raíz no tiene sentido, al parecer se ve bien considerando las restricciones. Saludos. --------------------  "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen.  Licenciado en Matemática (2021). Universidad de Concepción, Chile. |
|
|
|
 Apr 16 2008, 06:07 PM Apr 16 2008, 06:07 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 518 Registrado: 16-March 08 Miembro Nº: 17.054 Nacionalidad:  |
tengo que encontrar todos lo valores de x en los reales, tales que ![TEX: \[<br />\left| x \right| < x^2 <br />\]<br />](./tex/dcd5f2fe9d5dc9071dffe62301fa1493.png) esto hice: ![TEX: \[<br />\begin{gathered}<br /> \left| x \right| < x^2 /()^2 \hfill \\<br /> x^2 < x^4 / \cdot \frac{1}<br />{{x^2 }} \hfill \\<br /> 1 < x^2 /\sqrt {} \hfill \\<br /> 1 < \left| x \right| \hfill \\<br /> - 1 < x < 1 \hfill \\<br /> \hfill \\<br /> S = \left( { - 1,1} \right) \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/81afa5b54eda6d88c2e06b2cb00d7527.png) pero lo logico, es todo al reves xD, es decir todos los reales menos S, que hice mal? deberias empezar analizando el unico punto critico existente (el cero), y luego tomar valores cuando x<0 y cuando x>0. una vez analizado los casos por separados, los unes y tienes tu solucion |
|
|
|
 Apr 16 2008, 06:38 PM Apr 16 2008, 06:38 PM
Publicado:
#4
|
|
 Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Lo que tienes que tener claro es que 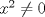 ya que si no estarías dividiendo por cero, luego lo correcto es extraer raíz, "no'' multiplicar por raíz, ya que multiplicar por el operador raíz no tiene sentido, al parecer se ve bien considerando las restricciones. Saludos. ya que si no estarías dividiendo por cero, luego lo correcto es extraer raíz, "no'' multiplicar por raíz, ya que multiplicar por el operador raíz no tiene sentido, al parecer se ve bien considerando las restricciones. Saludos. jaja ahi no multiplique por raiz, sino que la aplique aunque eso de que x^2 puede ser cero, tiene mucho sentido... deberias empezar analizando el unico punto critico existente (el cero), y luego tomar valores cuando x<0 y cuando x>0. una vez analizado los casos por separados, los unes y tienes tu solucion si entiendo, pero quiero saber en donde esta el error gracias! -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico  “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti ![TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />](/tex-image/662cf378c88b8d7170f7919ce7dc427a.png) |
|
|
|
 Apr 16 2008, 06:55 PM Apr 16 2008, 06:55 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
deberias empezar analizando el unico punto critico existente (el cero), y luego tomar valores cuando x<0 y cuando x>0. una vez analizado los casos por separados, los unes y tienes tu solucion Bueno, esto es lo que yo hice, revisen si estoy mal; ![TEX: \noindent Encontrar los valores de $x$ en los reales tales que; $|x|<x^2$\\<br />\hfill\\<br />Tenemos que elevar al cuadrado ya que no hay propiedad que nos ayude a simplificar el resultado, luego $|x|^2<x^4$, lo que es igual a $x^2<x^4$, ahora dividiendo por $x^2$, en donde se considera $x^2 \ne 0$, entonces nos queda $1<x^2$ , lo que es igual a decir $x^2>1$, extraendo raíz se obtiene; $|x|>1$ y esto por propiedades de valor absoluto nos arroja lo siguiente: $x>1\vee x<-1$ finalmente tú conjunto $\mathcal{S}$ es $\mathcal{S}=[1,+\infty[\cup ]-\infty,-1].$<br />](./tex/b9713aa17f4a011117b6f277782718bf.png)
--------------------  "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen.  Licenciado en Matemática (2021). Universidad de Concepción, Chile. |
|
|
|
 Apr 16 2008, 07:01 PM Apr 16 2008, 07:01 PM
Publicado:
#6
|
|
 Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
mmm...
pero por propiedad: ![TEX: \[<br />\left| x \right| > 1 \Leftrightarrow - 1 < x < 1 \Rightarrow - 1 < x \wedge x < 1<br />\]<br />](./tex/29fc3252657f735b73c1e673331aad86.png) eso es lo que yo tengo claro, o quizas me confundi y es: ![TEX: \[<br /> - 1 < x < 1 \Rightarrow - 1 < x \vee x < 1<br />\]<br />](./tex/58a345eae8ccb0a472b3bb22f3cbf749.png) llegando a tu respuesta, la que es la correcta -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico  “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti ![TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />](/tex-image/662cf378c88b8d7170f7919ce7dc427a.png) |
|
|
|
 Apr 16 2008, 07:12 PM Apr 16 2008, 07:12 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Si te sirve de algo, yo lo habría hecho así:
![TEX: \begin{equation*}\begin{aligned}<br />|x|&<x^2 \\<br />\\<br />\text{Si }x>0:\\<br />x&<x^2 \\<br />0&<x^2 -x\\<br />0&<x(x-1)\\<br />\\<br />\text{Si }x<0:\\<br />-x&<x^2 \\<br />0&<x^2 +x\\<br />0&<x(x+1)\\<br />\\<br />S=]\infty^-,-1[&\cup]1,\infty^+[<br />\end{aligned}\end{equation*}](./tex/7b8af4ea6d4d5623d4fbc3fcf3007e9f.png) Tu error está al final, esa propiedad es falsa cosa de darle un dígito, la propiedad es: 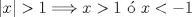
-------------------- |
|
|
|
 Apr 16 2008, 07:17 PM Apr 16 2008, 07:17 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
mmm... pero por propiedad: ![TEX: \[<br />\left| x \right| > 1 \Leftrightarrow - 1 < x < 1 \Rightarrow - 1 < x \wedge x < 1<br />\]<br />](./tex/f010f61fe4d7d8472a9d81581b192d25.png) eso es lo que yo tengo claro, o quizas me confundi y es: ![TEX: \[<br /> - 1 < x < 1 \Rightarrow - 1 < x \vee x < 1<br />\]<br />](./tex/dc68ea956dc9b1ff771980842648f263.png) llegando a tu respuesta, la que es la correcta Mi cuaderno de Álgebra I me dice que las propiedades son; 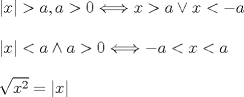
Mensaje modificado por julio el Apr 17 2008, 06:15 PM --------------------  "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen.  Licenciado en Matemática (2021). Universidad de Concepción, Chile. |
|
|
|
 Apr 16 2008, 07:47 PM Apr 16 2008, 07:47 PM
Publicado:
#9
|
|
 Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Si te sirve de algo, yo lo habría hecho así: ![TEX: \begin{equation*}\begin{aligned}<br />|x|&<x^2 \\<br />\\<br />\text{Si }x>0:\\<br />x&<x^2 \\<br />0&<x^2 -x\\<br />0&<x(x-1)\\<br />\\<br />\text{Si }x<0:\\<br />-x&<x^2 \\<br />0&<x^2 +x\\<br />0&<x(x+1)\\<br />\\<br />S=]\infty^-,-1[&\cup]1,\infty^+[<br />\end{aligned}\end{equation*}](./tex/7b8af4ea6d4d5623d4fbc3fcf3007e9f.png) Tu error está al final, esa propiedad es falsa cosa de darle un dígito, la propiedad es: 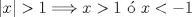 aah no sabia eso... Mi cuaderno de Álgebra I me dice que las propiedades son; 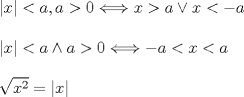 me parece que tienes un error de tipeo en la primera propiedad escrita, ya que revise en mi cuaderno y es: ![TEX: \[<br />\left| x \right| < \varepsilon \Leftrightarrow - \varepsilon < x < \varepsilon <br />\]<br />](./tex/77a576672a12de586f6e0fa5355fedcd.png) graciasa todos! entonces solo es un error conceptual Mensaje modificado por naxoobkn el Apr 16 2008, 08:45 PM -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico  “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti ![TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />](/tex-image/662cf378c88b8d7170f7919ce7dc427a.png) |
|
|
|
 Apr 16 2008, 09:22 PM Apr 16 2008, 09:22 PM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 15th April 2025 - 05:11 PM |












![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)


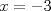 y
y 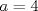 . De acuerdo a tu propiedad se tendria
. De acuerdo a tu propiedad se tendria 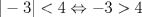 , lo que es falso.
, lo que es falso.