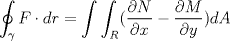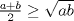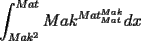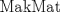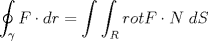|
|
|
|
|
|
|
 Apr 10 2012, 09:55 AM Apr 10 2012, 09:55 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
 Solucion: (Pendiente) 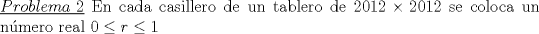 Solucion: (Pendiente) 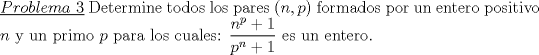 Solucion: (Pendiente) 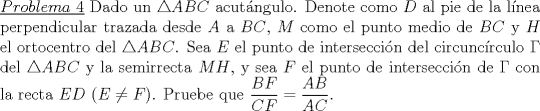 Solucion: (Pendiente) 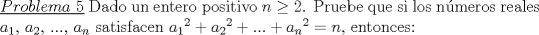 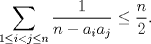 Solucion: (Pendiente) -------------------- |
|
|
|
Mensajes en este tema
 makmat APMO 2012 Apr 10 2012, 09:55 AM
makmat APMO 2012 Apr 10 2012, 09:55 AM
 El Geek Pregunta: ¿Para abordar el problema 3 se usa algo ... Apr 10 2012, 08:51 PM
El Geek Pregunta: ¿Para abordar el problema 3 se usa algo ... Apr 10 2012, 08:51 PM
 Alvaro Yonekura Baeza Disculpen, no sé adjuntar dibujos y recién aprendí... Apr 15 2012, 01:12 AM
Alvaro Yonekura Baeza Disculpen, no sé adjuntar dibujos y recién aprendí... Apr 15 2012, 01:12 AM  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 7th April 2025 - 09:34 PM |