|
|
|
|
|
|
|
 Apr 27 2011, 09:48 PM Apr 27 2011, 09:48 PM
Publicado:
#1
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 170 Registrado: 25-July 07 Miembro Nº: 7.812 |
Control 2 MA 2601, 2011/1 Prof. Salomé Martínez Aux. Edgardo Mathies y Sebastián Barbieri P1 a) Sea 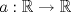 continua y de período continua y de período 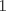 (1) 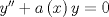 Demuestre que 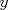 tiene período tiene período 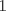 sí y solo si sí y solo si 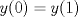 y y 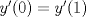 b) Suponga que 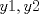 son una base de soluciones de (1) tales que son una base de soluciones de (1) tales que 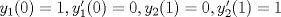 Demuestre que para todo Demuestre que para todo 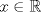 se tiene que se tiene que 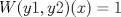 c) Demuestre que (1) tiene al menos una solución no trivial de período 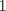 , si y solo si , si y solo si 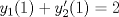 Ind: Para esto considere Ind: Para esto considere 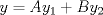 una solución de (1) y use las partes anteriores para deducir cuando una solución de (1) y use las partes anteriores para deducir cuando 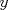 tiene período tiene período 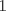 y es no trivial. y es no trivial.d) Determine todos los valores de 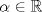 para los cuales la ecuación: para los cuales la ecuación: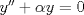 tiene soluciones no triviales de período 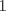 P2 a) Considere la ecuación 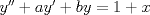 con 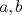 constantes, constantes, 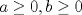 . Determine la solución general de la ecuación separando los casos . Determine la solución general de la ecuación separando los casos 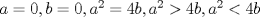 b) Resuelva el problema de valor inicial 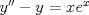 , con , con 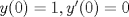 . (Ind: puede ser más eficiente usar variación de parámetros) . (Ind: puede ser más eficiente usar variación de parámetros)P3) a) Sean 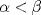 funciones continuas definidas en un intervalo funciones continuas definidas en un intervalo 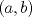 . Sea . Sea 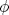 una solución no trivial de la ecuación una solución no trivial de la ecuación 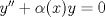 , y , y 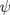 una solución no trivial de la ecuación una solución no trivial de la ecuación 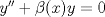 . Demuestre que si . Demuestre que si 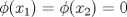 , con , con 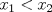 y y 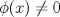 en en 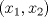 , entonces , entonces 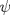 se anula en un punto en se anula en un punto en 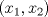 Ind: Considere el caso Ind: Considere el caso 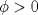 en en 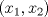 y suponga y suponga 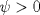 en en 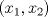 . Demuestre que . Demuestre que 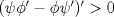 en en 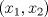 e integre e integre 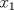 y y 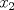 para obtener una contradicción. Explique como obtener el resultado en los otros casos. para obtener una contradicción. Explique como obtener el resultado en los otros casos.b) Suponga 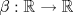 es continua, positiva y acotada por abajo, es decir es continua, positiva y acotada por abajo, es decir 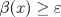 para todo para todo  , con , con 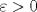 . Demuestre que cualquier solución de la ecuación . Demuestre que cualquier solución de la ecuación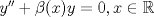 tiene un número infinito de ceros. Ind: Utilice la parte anterior, utilizando una ecuación adecuada (que tenga soluciones con infinitos ceros). |
|
|
|
Mensajes en este tema
 Chaparrón Control 2 EDO 2011/1 Apr 27 2011, 09:48 PM
Chaparrón Control 2 EDO 2011/1 Apr 27 2011, 09:48 PM
 Naxoo La P3 es muy del estilo Salomé May 9 2011, 03:33 PM
Naxoo La P3 es muy del estilo Salomé May 9 2011, 03:33 PM
 febomon 1a)
Supongamos que se cumple y(0)=y(1) y y´(0)... May 26 2011, 10:39 PM
febomon 1a)
Supongamos que se cumple y(0)=y(1) y y´(0)... May 26 2011, 10:39 PM
 Naxoo P3) Parte a)
\[\begin{gathered}
{... Aug 27 2011, 03:12 PM
Naxoo P3) Parte a)
\[\begin{gathered}
{... Aug 27 2011, 03:12 PM  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 06:13 AM |








