|
|
|
|
|
|
|
 Mar 13 2010, 12:48 PM Mar 13 2010, 12:48 PM
Publicado:
#1
|
|
|
Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 274 Registrado: 30-December 09 Miembro Nº: 64.740 Nacionalidad:  Colegio/Liceo:  Sexo:  |
3ª OLIMPIADA INTERNACIONAL DE MATEMÁTICA Veszprém, Hungría, 1961 Primera Prueba: Lunes 6 de julio de 1961 Problema 1: Resolver el siguiente sistema de ecuaciones: 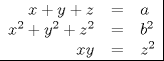 donde  y y  son constantes. De también las condiciones que deben cumplir son constantes. De también las condiciones que deben cumplir  y y  para que las soluciones del sistema sean números positivos distintos. para que las soluciones del sistema sean números positivos distintos.Problema 2: Sean  , ,  y y  los lados de un triángulo y los lados de un triángulo y 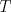 su área. Probar que su área. Probar que 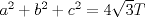 . ¿En qué casos se cumple ésta igualdad? . ¿En qué casos se cumple ésta igualdad?Problema 3: Resolver la ecuación 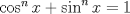 , donde , donde 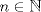 . .Segunda Prueba: Jueves 16 de julio de 1961 Problema 4: Considere un triángulo 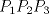 y un punto y un punto 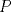 dentro del triángulo. Las rectas dentro del triángulo. Las rectas 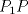 , , 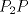 y y 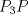 intercectan al lado opuesto en los puntos intercectan al lado opuesto en los puntos 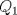 , , 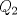 y y 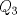 , respectivamente. Probar que, de los números de: , respectivamente. Probar que, de los números de: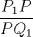 , , 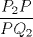 , , 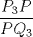 al menos uno sea 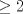 y al menos uno sea y al menos uno sea 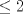 . .Problema 5: Construír un triángulo 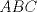 si si 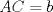 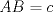 y y 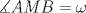 , donde , donde 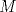 es el punto medio de es el punto medio de 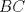 y y 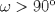 . Probar que una solución exista si y solo si: . Probar que una solución exista si y solo si: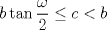 ¿En qué casos se cumple esta igualdad? Problema 6: Considere un plano  y tres puntos no colineales y tres puntos no colineales 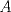 , , 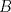 y y 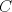 en el mismo lado de en el mismo lado de  . Suponga que el plano determinado por estos tres puntos no es paralelo a . Suponga que el plano determinado por estos tres puntos no es paralelo a  . En el plano se toman tres puntos arbitrarios . En el plano se toman tres puntos arbitrarios 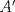 , , 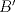 y y 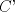 . Sean . Sean 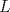 , , 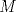 y y 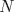 los puntos medios de los segmentos los puntos medios de los segmentos 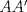 , , 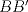 y y 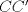 . Sea G el centroide del triángulo . Sea G el centroide del triángulo 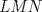 (Nótese que no consideramos las posiciones de (Nótese que no consideramos las posiciones de 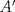 , , 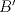 y y 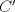 en las que éstas no forman un triángulo). ¿Cuál es el lugar geométrico del punto en las que éstas no forman un triángulo). ¿Cuál es el lugar geométrico del punto 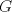 ya que ya que 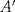 , , 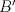 y y 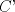 varían independientemente en el plano varían independientemente en el plano  . .Resumen de soluciones Mensaje modificado por einstenio16 el Jan 12 2023, 11:14 AM -------------------- He vuelto con las pilas cargaditas!!! |
|
|
|
Mensajes en este tema
 einstenio16 III IMO (1961) Mar 13 2010, 12:48 PM
einstenio16 III IMO (1961) Mar 13 2010, 12:48 PM
 Nabodorbuco En la pregunta 2 deberia decir
$a^{2}+b^{2}+... Feb 27 2011, 03:14 PM
Nabodorbuco En la pregunta 2 deberia decir
$a^{2}+b^{2}+... Feb 27 2011, 03:14 PM
 luis_fz eso mismo pensé después de haber postiado xD May 24 2011, 05:18 PM
luis_fz eso mismo pensé después de haber postiado xD May 24 2011, 05:18 PM

 El Geek Solo $n$ es natural, los catetos no nece... May 24 2011, 05:52 PM
El Geek Solo $n$ es natural, los catetos no nece... May 24 2011, 05:52 PM
 master_c Como a ni b no son fijos, dividimos el sistema en ... May 25 2011, 08:20 PM
master_c Como a ni b no son fijos, dividimos el sistema en ... May 25 2011, 08:20 PM
 panchovega_ Problema $2$ :
Sea $ABC$ un tr... Jan 24 2016, 03:29 PM
panchovega_ Problema $2$ :
Sea $ABC$ un tr... Jan 24 2016, 03:29 PM  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 7th April 2025 - 11:48 PM |







