|
|
|
|
|
|
|
 Jun 13 2009, 05:17 PM Jun 13 2009, 05:17 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Definicion: Sean
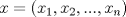 y y 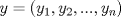 dos n-uplas. Diremos que dos n-uplas. Diremos que  mayoriza mayoriza 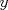 si se cumple que: si se cumple que: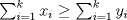 , , 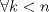  Desigualdad de Kamarata: Considere dos n-uplas 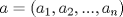 y y 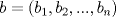 de numeros reales, tales que de numeros reales, tales que  mayoriza mayoriza  . Sea . Sea 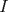 un intervalo que contiene a los 2n-reales un intervalo que contiene a los 2n-reales 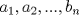 . Sea . Sea 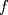 una funcion convexa en una funcion convexa en 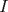 . Entonces se cumple que: . Entonces se cumple que: La desigualdad de Jensen es un caso especial de la Desigualdad de Karamata -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
Mensajes en este tema
 Kain #13 Desigualdad de Karamata Jun 13 2009, 05:17 PM
Kain #13 Desigualdad de Karamata Jun 13 2009, 05:17 PM
 Emi_C Si es concaba en diho intervalo, la desigualdad es... Jul 15 2010, 01:47 PM
Emi_C Si es concaba en diho intervalo, la desigualdad es... Jul 15 2010, 01:47 PM

 xD13G0x Si es concaba en diho intervalo, la desigualdad es... Jul 15 2010, 02:01 PM
xD13G0x Si es concaba en diho intervalo, la desigualdad es... Jul 15 2010, 02:01 PM
 El Geek No es de troll pero ¿Qué aplicación tiene esta cos... Jul 15 2010, 02:20 PM
El Geek No es de troll pero ¿Qué aplicación tiene esta cos... Jul 15 2010, 02:20 PM

 Hamon No es de troll pero ¿Qué aplicación tiene esta cos... Jul 15 2010, 02:22 PM
Hamon No es de troll pero ¿Qué aplicación tiene esta cos... Jul 15 2010, 02:22 PM
 Emi_C Lei el post y el titulo, y no supe si, era desigua... Jul 18 2010, 01:44 AM
Emi_C Lei el post y el titulo, y no supe si, era desigua... Jul 18 2010, 01:44 AM
 pobletex wena vale por la infomacion Jul 18 2010, 01:50 PM
pobletex wena vale por la infomacion Jul 18 2010, 01:50 PM
 Kaissa wena vale por la infomacion
no señor, no es info... Jul 18 2010, 02:28 PM
Kaissa wena vale por la infomacion
no señor, no es info... Jul 18 2010, 02:28 PM
 xD13G0x no señor, no es informacion.
lease como un propues... Jul 18 2010, 02:54 PM
xD13G0x no señor, no es informacion.
lease como un propues... Jul 18 2010, 02:54 PM  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th April 2025 - 03:07 AM |







