|
|
|
|
|
|
|
 Jan 11 2008, 09:26 PM Jan 11 2008, 09:26 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
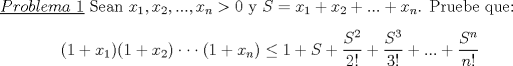 Soluciones: 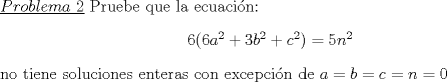 Solucion:  Solucion: (Pendiente) 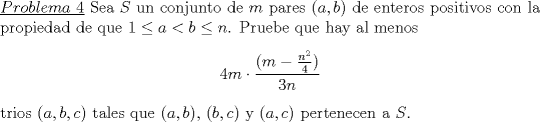 Solucion: (Pendiente)  Solucion: (Pendiente) Mensaje modificado por Luffy el Jun 2 2013, 10:20 PM |
|
|
|
Mensajes en este tema
 Luffy APMO 1989 Jan 11 2008, 09:26 PM
Luffy APMO 1989 Jan 11 2008, 09:26 PM
 ~Fatal_Collapse~ [tex=./tex/a9a17ba8aa7f8110f4ca677e7c941b57.png]... Mar 26 2010, 06:04 PM
~Fatal_Collapse~ [tex=./tex/a9a17ba8aa7f8110f4ca677e7c941b57.png]... Mar 26 2010, 06:04 PM

 Luffy Veamos que $2|5n^2$, y como $gcd(2,... Sep 27 2011, 12:01 AM
Luffy Veamos que $2|5n^2$, y como $gcd(2,... Sep 27 2011, 12:01 AM
 Javier Gómez L. \noindent\underline{$Problema... Sep 2 2012, 05:02 PM
Javier Gómez L. \noindent\underline{$Problema... Sep 2 2012, 05:02 PM
 Luffy \noindent\underline{$Problema... Jun 2 2013, 10:26 PM
Luffy \noindent\underline{$Problema... Jun 2 2013, 10:26 PM  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 7th April 2025 - 08:25 PM |






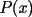 el polinomio
el polinomio ![TEX: \[<br />\prod\limits_{i = 1}^n {\left( {x + x_i } \right)} <br />\]](./tex/133368.gif) . Luego sus raíces son todos los
. Luego sus raíces son todos los 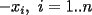 , y puede ser escrito de la forma
, y puede ser escrito de la forma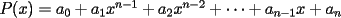
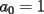 y, por las relaciones de Cardano-Vieta, cada
y, por las relaciones de Cardano-Vieta, cada 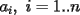 es igual a la suma de los productos de cada
es igual a la suma de los productos de cada 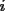 -combinación de
-combinación de 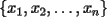 multiplicada por
multiplicada por 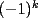 .
.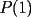 , o sea, igual a
, o sea, igual a ![TEX: \[<br />\sum\limits_{k = 0}^n {a_k } <br />\]](./tex/133377.gif)
![TEX: \[<br />a_k \le \frac{{S^k }}<br />{{k!}}<br />\]](./tex/133378.gif) , para
, para 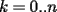 , o, lo que es equivalente, que
, o, lo que es equivalente, que ![TEX: \[<br />k!a_k \le S^k <br />\]](./tex/133380.gif) para los mismos
para los mismos 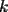
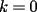 la igualdad es directa, y para
la igualdad es directa, y para 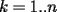 , recordamos cuatro cosas:
, recordamos cuatro cosas: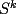 no aparecerán sumandos negativos, pues cada sumando dentro de
no aparecerán sumandos negativos, pues cada sumando dentro de 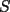 no lo es;
no lo es;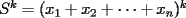 , cada
, cada 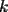 -combinación de los
-combinación de los 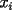 aparece sumada
aparece sumada 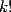 veces; *
veces; *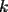 es par, la suma de los productos de las
es par, la suma de los productos de las 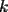 combinaciones de los
combinaciones de los 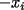 , igual a
, igual a 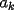 , es también igual a la correspondiente suma de los
, es también igual a la correspondiente suma de los 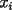 ;
;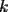 es impar, la suma de los productos de las
es impar, la suma de los productos de las 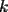 combinaciones de los
combinaciones de los 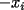 , igual a
, igual a 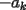 , es opuesta en signo a la correspondiente suma de los
, es opuesta en signo a la correspondiente suma de los 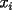 .
.![TEX: \[<br />k!a_k \le S^k <br />\]](./tex/133400.gif) para
para 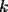 par, y usando los puntos 1, 2 y 4 para
par, y usando los puntos 1, 2 y 4 para 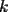 impar.
impar.![TEX: \[<br />\sum\limits_{k = 0}^n {\frac{{S^k }}<br />{{k!}} \ge \sum\limits_{k = 0}^n {a_k } = P\left( 1 \right) = \prod\limits_{i = 1}^n {\left( {1 + x_i } \right)} } <br />\]](./tex/133403.gif)