Divisibilidad y más - Foro fmat.cl

Divisibilidad y más, Parte 1

pelao_malo Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 3 2007, 03:33 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad: Colegio/Liceo: Sexo:	hola amigos de fmat! weno, yo quiero ahora compartir con ustedes un par de cosillas, que nunca están demás en el arsenal de los que les gusta la matemática y el por qué de algunas cositas básicas. 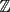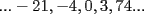La Divisibilidad de los Números Para no tener dudas en la lectura, los enteros se denotan por $TEX: $\mathbb{Z}$$ y algunos de estos son $TEX: $...-21,-4,0,3,74...$$ . 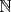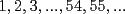Los naturales de denotan por $TEX: $\mathbb{N}$$ y algunos de estos son $TEX: $1,2,3,...,54,55,...$$ . 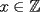Diremos $TEX: $x\in{\mathbb{Z}}$$ si $TEX: $x$$ es un número que pertenece a los enteros. 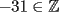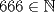Por ejemplo, $TEX: $-31\in{\mathbb{Z}}$$ y $TEX: $666\in{\mathbb{N}}$$ . Ahora, para empezar, debemos definir que es divisibilidad. 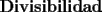$TEX: \noindent \bf{Divisibilidad}$ $TEX: \noindent Si $a,b\in{\mathbb{Z}}$, diremos que un n\'umero $a$ es divisible por un n\'umero $b$, con $b\not=0$, si $a=bk$, con $k\in{\mathbb{Z}}$. Lo denotaremos por $b\mid a$ ($b$ divide al n\'umero $a$).\\<br /><br />\noindent Ejemplos:\\<br />$4\mid 28$, porque $28=4\cdot 7$, y $7$ es un entero.\\<br />$5\mid 200$, porque $200=5\cdot 40$ $40$ que es un entero.\\<br />$6\not \|\ 34$ porque $34=6k$ donde $k$ no es entero.\\<br /><br />\noindent Podemos usar un m\'etodo muy bonito para calcular si n\'umeros grandes son divisibles por alg\'un n\'umero, lo presentar\'e a continuaci\'on:\\<br /><br />\noindent Deseamos saber si $n=34026$ es divisible en $6$, entonces, lo que hacemos es encontrar un m\'ultiplo de $6$ conocido suficientemente grande como para restarselo a $n$ y as\'i poder analizarlo m\'as r\'apido.\\<br />Al ojo se ve que es $30000$, entonces se lo restamos y obtenemos $34026-30000=4026$, ahora le restamos otro n\'umero m\'ultiplo de $6$ cercano, que se podr\'ia decir que es $3600$, entonces queda $4026-3600=426$, si a este n\'umero le restamos $420$ que es m\'ultiplo de $6$, obtenemos $6$, que es divisible en $6$.<br />Podemos concluir as\'i que $34026$ es divisible en $6$, ya que todos los pasos son reversibles, y como $6=6\cdot 1$, $420=6\cdot 70$, $3600=6\cdot 600$ y $30000=6\cdot 5000$; y los sumamos, quedando de la forma $6(1+70+600+5000)$. En general, podemos averiguar si un n\'umero $a$ es divisible en $b$, rest\'andole continuamente m\'ultiplos de $b$ para as\'i lograr legar a un n\'umero peque\~no y decir si $a$ es divisible en $b$. Si es que el \'ultimo n\'umero peque\~no llegamos no es un m\'ultiplo de $b$, implica que $a\not \|\ b$.\\<br /><br />\noindent Sabiendo la definici\'on y ese truquito, podemos continuar definiendo un t\'ermino crucial en el desarrollo de este tema$ $TEX: $\bf{Congruencia}\\$$ $TEX: \noindent Si $a,b\in{\mathbb{Z}}$ y $n\in{\mathbb{N}}$, son tales que $n\mid (a-b)$, entonces decimos $$a\equiv b(n)$$ y se lee \emph{$a$ es congruente a $b$ en m\'odulo $n$}$ $TEX: \noindent Repasaremos unas propiedades de la congruencia, que nos dar\'an una s\'olida base para poder deducir divisibilidades.\\<br /><br />\noindent 1.- Si $a\equiv b(n)$, y $c\in{\mathbb{Z}}$, entonces $a+c\equiv b+c(n)$.\\<br /><br />\noindent Demostraci\'on: S\'olo debemos notar que $$a+c-(b+c)=a+c-b-c=a-b$$ entonces $$n\mid (a-b)\Longrightarrow n\mid (a+c)-(b+c)\Longrightarrow a+c\equiv b+c(n)$$\\<br /><br />\noindent 2.- Si $a\equiv b(n)$, y $c\equiv d(n)$, entonces $ac\equiv bd(n)$.\\<br /><br />\noindent Demostraci\'on: Si $$a\equiv b(n)\Longrightarrow a=b+kn$$ para alg\'un $k\in{\mathbb{Z}}$, entonces $$c\equiv d(n)\Longrightarrow c=d+nl$$ con $l\in{\mathbb{Z}}$. Eso implica que $$ab=knnl+knd+bnl+cd\Longrightarrow ab-cd=n\underbrace{(knl+kd+bl)}_{entero}$$ entonces $ab\equiv bc(n)$.\\<br /><br />\noindent 3.- Si $a\equiv b(n)$, y $k\in{\mathbb{N}}$, entonces $a^k\equiv b^k(n)$.\\<br /><br />\noindent Demostraci\'on: Podemos multiplicar la congruencia $a\equiv b(n)$ por si misma $k$ veces (gracias a la propiedad $2$) para obtener $a^k\equiv b^k(n)$.$ --------------------------------------------------------------------------------------------------------------------- Ya visto lo anteriormente expuesto, podemos ver lo que realmente quería compartir. $TEX: \noindent Todo n\'umero que analizaremos a continuaci\'on, ser\'a en la base $10$.\\<br />Eso significa que cualquier n\'umero $x$ puede ser escrito como una suma de t\'erminos de la forma $10^ia_i$ con $a_i$ el d\'igito en la posici\'on $a+1$.\\<br />Por ejemplo $$5782=5\cdot 10^3+7\cdot 10^2+8\cdot 10^1+2$$<br />Teniendo esto en cuenta, podemos continuar nuestra lectura$ $TEX: \noindent Sabemos que un n\'umero es divisible en $2$, si su \'ultima cifra lo es (par).\\<br />Sabemos que un n\'umero es divisible en $4$, si sus \'ultimas $2$ cifras lo son.\\<br />Tambi\'en se sabe que para que un n\'umero sea div. en $8$, sus \'ultimas $3$ cifras deben serlo.\\<br />Entonces, como para seguir un patr\'on, podemos decir:\\<br />Para que un número sea divisible en $2^k$, sus últimas $k$ cifras deben serlo.$ Ahora, ¿Cómo demostrarlo?. 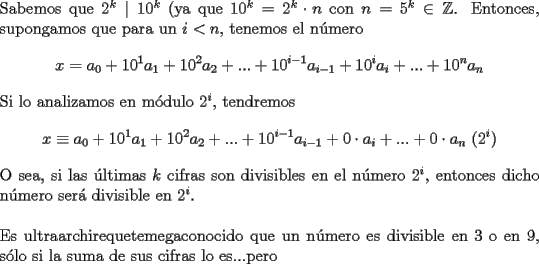$TEX: \noindent Sabemos que $2^k\mid 10^k$ (ya que $10^k=2^k\cdot n$ con $n=5^k\in{\mathbb{Z}}$.<br />Entonces, supongamos que para un $i<n$, tenemos el n\'umero $$x=a_0+10^1a_1+10^2a_2+...+10^{i-1}a_{i-1}+10^ia_i+...+10^na_n$$ Si lo analizamos en m\'odulo $2^i$, tendremos $$x\equiv a_0+10^1a_1+10^2a_2+...+10^{i-1}a_{i-1}+0\cdot a_i+...+0\cdot a_n\ (2^i)$$ O sea, si las \'ultimas $k$ cifras son divisibles en el n\'umero $2^i$, entonces dicho n\'umero ser\'a divisible en $2^i$.\\<br /><br />\noindent Es ultraarchirequetemegaconocido que un n\'umero es divisible en $3$ o en $9$, s\'olo si la suma de sus cifras lo es...pero$ ¿Será cierto? $TEX: \noindent Sea $$x=a_0+10^1a_1+10^2a_2+...+10^na_n$$ Notemos que $10\equiv 1(3)\Longrightarrow 10^j\equiv 1^j\equiv 1(3)$ con un $j\in{\mathbb{N}}$. Entonces, analizando $x$ en m\'odulo $3$ tenemos $$x\equiv a_0+1\cdot a_1+1\cdot a_2+...+1\cdot a_n(3)$$ Concluyendo que si la suma de las cifras de $x$ es divisible en $3$, $x$ tambi\'en lo ser\'a. An\'alogamente, $10\equiv 1(9)\Longrightarrow 10^j\equiv 1(9)$, demostrando lo mismo para $9$. Pero por qu\'e aqu\'i no podemos decir: $x$ es div. en $3^j$ solo si la suma de sus cifras lo son... porque $3$ y $9$ son los \'unicos n\'umeros que cumplen $10\equiv 1$ en dicho m\'odulo.\\<br /><br />\noindent La divisibilidad en $5$ nos dice algo similar a la del $2$, o sea, las \'ultimas $j$ cifras deben ser divisibles en $x$ para que $x$ sea divisible en $5^j$...Esta aseveraci\'on es cierta, y se demuestra de manera muy similar a la de $2^k$ que hicimos anteriormente, solo cambia eñ n\'umero en dicho an\'alisis, pero es la misma regla.\\<br /><br />\noindent Si usted de esos emprendedores que les gusta averiguar todo, dem\'as que se sabe la regla de divisibilidad por $11$, pero es mas o menos complicada. Pero debes animarlo a demostrarla! =D!.\\<br /><br />\noindent Sabemos que $10\equiv -1(11)$, entonces si $n\in{\mathbb{N}}$ tenemos $$(-1)^{2n}=1$$ $$(-1)^{2n-1}=-1$$ de donde podemos concluir que $$10^{2n}\equiv 1(11)$$ $$10^{2n-1}\equiv -1(11)$$ Invoquemos nuevamente a nuestro requeteusado n\'umero $$x=a_0+10^1a_1+10^2a_2+10^3a_3+...+10^na_n$$ <br />Contin\'ua..........$ -------------------- $TEX: $\sqrt{5}=41$$