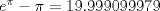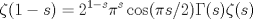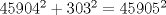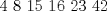Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



> Propuesto "hereda condiciones del límite"
Laðeralus
mensaje Dec 7 2020, 09:55 PM
Publicado: #1


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 947
Registrado: 28-September 07
Desde: Santiago
Miembro Nº: 10.639
Nacionalidad:
Universidad: Universidad Diego Portales
Sexo:



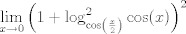
Calcule TEX: $\displaystyle \lim_{x \to 0} \left( 1+\log^2_{\cos \left( \frac{x}{2}\right)} \cos(x) \right)^2 $
Go to the top of the page
 
+Quote Post
 
 Start new topic
Respuestas
Laðeralus
mensaje Dec 8 2020, 02:36 AM
Publicado: #2


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 947
Registrado: 28-September 07
Desde: Santiago
Miembro Nº: 10.639
Nacionalidad:
Universidad: Universidad Diego Portales
Sexo:



Hermosa solución wub.gif
Yo me fui por el camino de tierra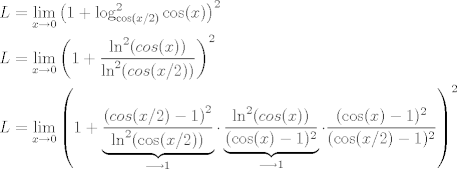

TEX: <br />\begin{align*}<br />L &= \lim_{x\to 0} \left( 1+\log^2_{\cos(x/2)} \cos(x) \right)^2 \\<br />L &= \lim_{x\to 0} \left( 1+\frac{\ln^2(cos(x))}{\ln^2 (cos(x/2))} \right)^2 \\<br />L &= \lim_{x\to 0} \left( 1 + \underbrace{\frac{\left(cos(x/2)-1\right)^2}{\ln^2(\cos(x/2))}}_{\longrightarrow 1} \cdot \underbrace{\frac{\ln^2(cos(x))}{(\cos(x)-1)^2}}_{\longrightarrow 1} \cdot \frac{(\cos(x)-1)^2}{(\cos(x/2)-1)^2} \right)^2<br />\end{align*}

Falta calcular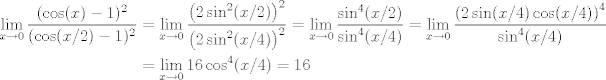
TEX: \begin{align*}<br />\lim_{x\to 0} \frac{(\cos(x)-1)^2}{(\cos(x/2)-1)^2} &= \lim_{x\to 0} \frac{\left(2\sin^2(x/2)\right)^2}{\left(2\sin^2(x/4)\right)^2} = \lim_{x\to 0} \frac{\sin^4(x/2)}{\sin^4(x/4)} = \lim_{x\to 0} \frac{\left(2\sin(x/4)\cos(x/4)\right)^4}{\sin^4(x/4)} \\<br />&= \lim_{x\to 0} 16\cos^4(x/4) = 16<br />\end{align*}

Por lo tanto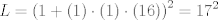
TEX: $\displaystyle L = \left(1+(1)\cdot (1)\cdot (16)\right)^2 = 17^2$

Mensaje modificado por Laðeralus el Dec 8 2020, 02:38 AM
Go to the top of the page
 
+Quote Post
2.718281828
mensaje Dec 8 2020, 12:56 PM
Publicado: #3


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 1.879
Registrado: 27-December 07
Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR
Miembro Nº: 14.122
Nacionalidad:
Universidad: Universidad Catolica de Chile
Sexo:



CITA(Laðeralus @ Dec 8 2020, 02:36 AM) *
Hermosa solución wub.gif
Yo me fui por el camino de tierra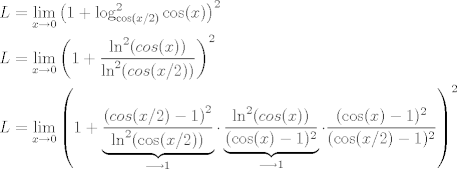

TEX: <br />\begin{align*}<br />L &= \lim_{x\to 0} \left( 1+\log^2_{\cos(x/2)} \cos(x) \right)^2 \\<br />L &= \lim_{x\to 0} \left( 1+\frac{\ln^2(cos(x))}{\ln^2 (cos(x/2))} \right)^2 \\<br />L &= \lim_{x\to 0} \left( 1 + \underbrace{\frac{\left(cos(x/2)-1\right)^2}{\ln^2(\cos(x/2))}}_{\longrightarrow 1} \cdot \underbrace{\frac{\ln^2(cos(x))}{(\cos(x)-1)^2}}_{\longrightarrow 1} \cdot \frac{(\cos(x)-1)^2}{(\cos(x/2)-1)^2} \right)^2<br />\end{align*}

Falta calcular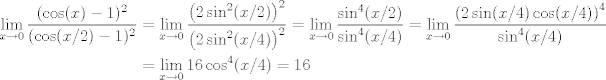
TEX: \begin{align*}<br />\lim_{x\to 0} \frac{(\cos(x)-1)^2}{(\cos(x/2)-1)^2} &= \lim_{x\to 0} \frac{\left(2\sin^2(x/2)\right)^2}{\left(2\sin^2(x/4)\right)^2} = \lim_{x\to 0} \frac{\sin^4(x/2)}{\sin^4(x/4)} = \lim_{x\to 0} \frac{\left(2\sin(x/4)\cos(x/4)\right)^4}{\sin^4(x/4)} \\<br />&= \lim_{x\to 0} 16\cos^4(x/4) = 16<br />\end{align*}

Por lo tanto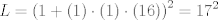
TEX: $\displaystyle L = \left(1+(1)\cdot (1)\cdot (16)\right)^2 = 17^2$


Esta super bacan tambien!

Ultimamente le he pegado harto a las notaciones de la o chica y la O grande. (Notaciones de Landau). ¿Por qué no lo enseñan en cursos de calculo estándar del pais?... es tan, pero tan util... Tantas cosas se pueden expresar fácilmente con esa notación, partiendo de Taylor, sumas, etc.

Saludos
Claudio.


--------------------
Claudio Henriquez Tapia
Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM
Candidato a Doctor en Estadística UC. Campus San Joaquin
Si todo sale bien, estaría defendiendo en Julio 2024.

[indent]
everywhere at the end of FMAT
ｆｍａｔ　ｎｅｅｄｓ　.... To Survive...
3ch03s facts:

Frases para el bronce by 3ch03s:

Fmat dejame subir mas citas!
TB-3030303
que es YTP-Tennis:
Go to the top of the page
 
+Quote Post
SuKeVinBellaKo
mensaje Dec 9 2020, 07:59 AM
Publicado: #4


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 524
Registrado: 2-October 13
Miembro Nº: 122.939
Nacionalidad:
Sexo:



CITA(2.718281828 @ Dec 8 2020, 12:56 PM) *
Esta super bacan tambien!

Ultimamente le he pegado harto a las notaciones de la o chica y la O grande. (Notaciones de Landau). ¿Por qué no lo enseñan en cursos de calculo estándar del pais?... es tan, pero tan util... Tantas cosas se pueden expresar fácilmente con esa notación, partiendo de Taylor, sumas, etc.

Saludos
Claudio.


imagino que por pedagogia cuando se ensena Taylor los profesores prefieren escribir todos los terminos, y mencionar que los terminos restantes contribuyen menos. Entiendo que la notacion O es util pa los limites, pero imagino que podria confundir a la gente. A veces yo igual prefiero escribir las cosas mas pajeramente pero sin introducir conceptos. Imagino que es algo de estilo.

Cuando tuve mi curso de python del MITx online hace unos anyos, me vi forzado a aprenderla porque tuve que estudiar complejidad computacional. Pero al parecer en mates se puede sobrevivir sin ella.
Go to the top of the page
 
+Quote Post
snw
mensaje Dec 9 2020, 10:00 AM
Publicado: #5


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 2.139
Registrado: 11-June 08
Desde: UK
Miembro Nº: 26.837
Nacionalidad:
Colegio/Liceo: Instituto Nacional
Universidad: Universidad de Chile-FCFM
Sexo:



CITA(SuKeVinBellaKo @ Dec 9 2020, 08:59 AM) *
imagino que por pedagogia cuando se ensena Taylor los profesores prefieren escribir todos los terminos, y mencionar que los terminos restantes contribuyen menos. Entiendo que la notacion O es util pa los limites, pero imagino que podria confundir a la gente. A veces yo igual prefiero escribir las cosas mas pajeramente pero sin introducir conceptos. Imagino que es algo de estilo.

Cuando tuve mi curso de python del MITx online hace unos anyos, me vi forzado a aprenderla porque tuve que estudiar complejidad computacional. Pero al parecer en mates se puede sobrevivir sin ella.


No sé, ah. Yo la ocupo mucho en combinatoria, también se usa mucho en proba y teoría analítica de números


--------------------
blep
Go to the top of the page
 
+Quote Post
Laðeralus
mensaje Dec 9 2020, 03:03 PM
Publicado: #6


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 947
Registrado: 28-September 07
Desde: Santiago
Miembro Nº: 10.639
Nacionalidad:
Universidad: Universidad Diego Portales
Sexo:



CITA(snw @ Dec 9 2020, 10:00 AM) *
No sé, ah. Yo la ocupo mucho en combinatoria, también se usa mucho en proba y teoría analítica de números

Yo creo que se refería a las matemáticas básicas de ingeniería (cálculos, álgebras, edo). En efecto, las o'es no son necesarias para esos cursos, pero estoy de acuerdo que son útiles en ramos de especialidad.
A mi me sirvió brígido en optimización combinatoria. Las o'es se me salían por las orejas

Mensaje modificado por Laðeralus el Dec 9 2020, 08:04 PM
Go to the top of the page
 
+Quote Post

Mensajes en este tema
Laðeralus   Propuesto "hereda condiciones del límite"   Dec 7 2020, 09:55 PM
2.718281828   Usando expansion hasta segundo orden notando que ...   Dec 8 2020, 12:34 AM
Laðeralus   Esta super bacan tambien! Ultimamente le he p...   Dec 8 2020, 02:48 PM
SuKeVinBellaKo   Yo creo que se refería a las matemáticas básicas d...   Dec 10 2020, 01:21 AM
Laðeralus   Claro, me referia al pregrado. Cuando uno se espec...   Dec 10 2020, 04:18 PM
2.718281828   o(f(x)) es machista y patriarcal, mejor e(f(x)) xd...   Dec 17 2020, 09:02 PM
Laðeralus   me O(fende) me O(prime)   Dec 19 2020, 12:02 AM
SuKeVinBellaKo   No sé, ah. Yo la ocupo mucho en combinatoria, tamb...   Dec 10 2020, 01:17 AM
SuKeVinBellaKo   ɒviƚimiɿq ɒ| ɘb ꙅ...   Dec 8 2020, 02:46 AM
Juan Illanes   ¿Cómo funciona la notación de Landau?   Dec 8 2020, 08:23 PM
SuKeVinBellaKo   ¿Cómo funciona la notación de Landau? ahi estan t...   Dec 9 2020, 08:05 AM

 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 21st April 2025 - 01:09 AM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.