|
|
|
|
|
|
|
 Feb 11 2009, 05:49 PM Feb 11 2009, 05:49 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Resuelva en
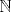 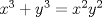 cualquiera puede responder! |
|
|
|
 |
Respuestas
 Feb 12 2009, 12:05 PM Feb 12 2009, 12:05 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Estás diciendo que todas las soluciones son de la forma (ky,y), con k natural. Es decir: estás diciendo que x debe ser múltiplo de y.
No estás justificando esa suposición, por lo tanto todavía esperamos una solución para el problema -------------------- |
|
|
|
 Feb 12 2009, 12:14 PM Feb 12 2009, 12:14 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 309 Registrado: 2-December 08 Desde: Cerro Navia Miembro Nº: 40.183 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Estás diciendo que todas las soluciones son de la forma (ky,y), con k natural. Es decir: estás diciendo que x debe ser múltiplo de y. No estás justificando esa suposición, por lo tanto todavía esperamos una solución para el problema Justificación: Caso 1: Si x e y son impares: Este caso no puede ocurrir ya que 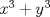 sería par, y sería par, y 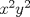 sería impar. sería impar.Caso 2: x par, y impar (S.P.G): Este caso no puede ocurrir ya que 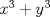 sería impar, y sería impar, y 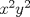 sería par. sería par.Luego el único caso posible de solución es que x e y sean pares. Luego es posible encontrar un 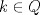 (sorry), que cumple la propiedad de que (sorry), que cumple la propiedad de que 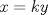 Pd: Creo que con eso debe quedar claro. Saludos. |
|
|
|
Mensajes en este tema
 Felipe_ambuli Resuelva en N Feb 11 2009, 05:49 PM
Felipe_ambuli Resuelva en N Feb 11 2009, 05:49 PM
 La.Catiita Me siento tonta...
no logro razonar...
... Feb 11 2009, 06:53 PM
La.Catiita Me siento tonta...
no logro razonar...
... Feb 11 2009, 06:53 PM
 psepulveda Solución:
\[
\begin{gathered}
{... Feb 11 2009, 11:23 PM
psepulveda Solución:
\[
\begin{gathered}
{... Feb 11 2009, 11:23 PM
 Mel S. Resuelva en [tex=./tex/df10dfb39b3605cb795042cb89c... Dec 3 2009, 05:44 PM
Mel S. Resuelva en [tex=./tex/df10dfb39b3605cb795042cb89c... Dec 3 2009, 05:44 PM
 xD13G0x la solucion esta correcta, bienvenido al foro Dec 3 2009, 10:00 PM
xD13G0x la solucion esta correcta, bienvenido al foro Dec 3 2009, 10:00 PM
 Pedantic Anarchy Aca va otra respuesta,
$$x^3+y^3=x^2y^2... Feb 20 2010, 12:30 AM
Pedantic Anarchy Aca va otra respuesta,
$$x^3+y^3=x^2y^2... Feb 20 2010, 12:30 AM
 Pedantic Anarchy . Mar 4 2010, 02:07 PM
Pedantic Anarchy . Mar 4 2010, 02:07 PM
 xD13G0x Aqui otra solucion:
Supongamos que $x$ y... Dec 28 2011, 02:20 PM
xD13G0x Aqui otra solucion:
Supongamos que $x$ y... Dec 28 2011, 02:20 PM

 snw Aqui otra solucion:
Supongamos que $x$ y... Dec 28 2011, 06:17 PM
snw Aqui otra solucion:
Supongamos que $x$ y... Dec 28 2011, 06:17 PM
 Maxooon Qué es e sub p? Apr 28 2013, 03:37 PM
Maxooon Qué es e sub p? Apr 28 2013, 03:37 PM
 Adrianocor que es e sub p? Aug 21 2014, 05:21 PM
Adrianocor que es e sub p? Aug 21 2014, 05:21 PM  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 27th April 2025 - 02:33 PM |










