|
|
|
|
|
|
|
 Aug 18 2005, 05:42 PM Aug 18 2005, 05:42 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Esta semana vamos a conocer la Prueba de Clasificación de la Olimpiada Nacional. Aún así no es la idea perder la costumbre de la lista semanal de problemas. Comienzo con uno simpático, pero algo laborioso...
Problema 1: Tenemos un 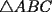 equilátero. En el día 0, a las 8:00 AM, hay una masa 1, concentrada en el punto equilátero. En el día 0, a las 8:00 AM, hay una masa 1, concentrada en el punto 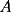 (los puntos (los puntos 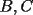 no tienen masa, o sea la masa en ellos vale 0 a las 8:00 AM del día 0). Para cada no tienen masa, o sea la masa en ellos vale 0 a las 8:00 AM del día 0). Para cada 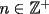 , ocurren las siguientes cosas: , ocurren las siguientes cosas:
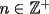 , determine la distribución de masa (en cada vértice) en el día , determine la distribución de masa (en cada vértice) en el día  , a las 8:00 AM. Como sugerencia, encuentre la distribución de los primeros días, cosa de ver si está entendiendo el problema. Toda la información relevante está a las 8:00 AM. Luego intente deducir una fórmula general. Puede ser de mucha ayuda asignar las siguientes incógnitas: , a las 8:00 AM. Como sugerencia, encuentre la distribución de los primeros días, cosa de ver si está entendiendo el problema. Toda la información relevante está a las 8:00 AM. Luego intente deducir una fórmula general. Puede ser de mucha ayuda asignar las siguientes incógnitas:El día  , a las 8:00 AM, tenemos una masa , a las 8:00 AM, tenemos una masa 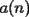 en el vértice en el vértice 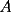 , una masa , una masa 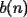 en el vértice en el vértice 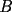 , y una masa , y una masa 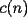 en el vértice en el vértice 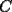 . .
-------------------- |
|
|
|
 |
Respuestas
 Aug 26 2005, 10:43 PM Aug 26 2005, 10:43 PM
Publicado:
#2
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 116 Registrado: 14-May 05 Desde: Buin, Santiago Miembro Nº: 26 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 5: Encuentre todos los pares (a,b) de enteros positivos, tales que un tablero cuadriculado de a×b casillas puede ser cubierto por figuras T. Debe ser cubierto totalmente, sin superposiciones y sin salir las figuras T del tablero. Una figura T ocupa cuatro casillas, conectadas entre sí formando una letra T.
Antes que nada, tenemos que estar claros que como el 4 es par, entonces a*b debe ser par. a*b=2k. Pintemos el tablero de axb como tablero de ajedrez (que original  Supongamos que para llenar el tablero ocupamos x piezas T1 e y piezas T2. Entonces: 3x+y = ab/2 ==> casilleros negros 3y+x= ab/2 ==> casilleros blancos. Además, si sumamos ambos, tenemos que 4x+4y=ab 4(x+y)=ab x+y = ab/4, pero como x=y, entonces, podemos decir que x=ab/8 Luego, como ab=2k, tenemos que x= 2k/8 ==> x=k/4. Por lo tanto, concluimos que a=4t y b=4r. Y eso ps.... sería todo...fin....se acabó... Otra manera, que deja un poco más de dudas, pero igual sería util, es formar el tablero de 4x4 y luego, podemos ir pegandolos, entonces, tenemos que se podria para todos los a=4t y b=ur Ia no+....au revoir QUEPD by mAsTeR® --------------------   "Lo que no entiendes hoy lo comprenderás mañana" |
|
|
|
Mensajes en este tema
 xsebastian Semana del 18 al 24 de Agosto Aug 18 2005, 05:42 PM
xsebastian Semana del 18 al 24 de Agosto Aug 18 2005, 05:42 PM
 xsebastian Un problema 2 que sirve mejor como práctica para e... Aug 18 2005, 05:59 PM
xsebastian Un problema 2 que sirve mejor como práctica para e... Aug 18 2005, 05:59 PM
 Kenshin Y aca va el regalito de la semana...solo para los ... Aug 19 2005, 10:12 AM
Kenshin Y aca va el regalito de la semana...solo para los ... Aug 19 2005, 10:12 AM
 Kenshin Problema 4
Probar que existen enteros [tex=./tex/7... Aug 19 2005, 10:24 AM
Kenshin Problema 4
Probar que existen enteros [tex=./tex/7... Aug 19 2005, 10:24 AM
 xsebastian Generalicemos un problema de la olimpiada nacional... Aug 22 2005, 09:58 AM
xsebastian Generalicemos un problema de la olimpiada nacional... Aug 22 2005, 09:58 AM
 xsebastian Problema 6: Sea $\overline{AH}$ una... Aug 22 2005, 10:03 AM
xsebastian Problema 6: Sea $\overline{AH}$ una... Aug 22 2005, 10:03 AM
 Caetano Solucion al problema 6:
Trazemos los segmentos OA... Aug 22 2005, 10:26 PM
Caetano Solucion al problema 6:
Trazemos los segmentos OA... Aug 22 2005, 10:26 PM
 Kenshin Y aca viene El desafio de la Semana
Para cada ent... Aug 23 2005, 11:05 PM
Kenshin Y aca viene El desafio de la Semana
Para cada ent... Aug 23 2005, 11:05 PM

 Claudio Espinoza Problema 1
Notemos que la masa total en los 3 vér... Oct 23 2006, 04:47 PM
Claudio Espinoza Problema 1
Notemos que la masa total en los 3 vér... Oct 23 2006, 04:47 PM
 xsebastian inicialmente, es obvio que $ab=4c$, si u... Aug 27 2005, 09:13 AM
xsebastian inicialmente, es obvio que $ab=4c$, si u... Aug 27 2005, 09:13 AM  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 22nd April 2025 - 05:58 AM |





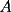 , uno de los grupos parte desde
, uno de los grupos parte desde 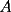 hacia
hacia 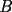 , y el otro desde
, y el otro desde 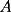 hasta
hasta 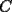 )
)


