|
|
|
|
|
|
|
 Apr 19 2006, 07:07 PM Apr 19 2006, 07:07 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad:  Colegio/Liceo:  Sexo:  |
2º OLIMPIADA DE MATEMÁTICAS DEL CONO SUR Argentina, 1991 Primera Prueba Problema 1: Sean 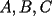 tres puntos no colineales, y tres puntos no colineales, y 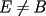 un punto cualquiera, con un punto cualquiera, con 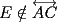 . Construya los paralelógramos . Construya los paralelógramos 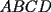 y y 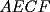 (ambos en ese orden). Pruebe que (ambos en ese orden). Pruebe que 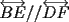 Problema 2: Dos personas: 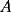 y y 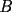 , practican el siguiente juego: , practican el siguiente juego: 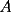 comienza eligiendo un natural y luego, cada jugador en su turno, dice un número de acuerdo al reglamento: comienza eligiendo un natural y luego, cada jugador en su turno, dice un número de acuerdo al reglamento:• Si el último número mencionado fue impar, el jugador suma 7 a ese número • Si el último número mencionado fue par, el jugador lo divide por 2. Gana el jugador que repite el número elegido inicialmente. Encuentre, justificadamente, todos los números que 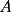 puede elegir para ganar. puede elegir para ganar.Problema 3: Se sabe que el número de soluciones 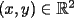 del siguiente sistema de ecuaciones es finito. Pruebe que dicho número de soluciones es par. del siguiente sistema de ecuaciones es finito. Pruebe que dicho número de soluciones es par.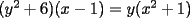 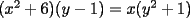 Segunda Prueba Problema 4: En cada casilla de un tablero de 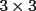 hay un botón, que puede estar de color rojo o verde. Si se oprime un botón en el borde del tablero, él y todos sus vecinos cambian de color. Si se oprime el botón central, cambian de color sus ocho vecinos, pero él mantiene su color. Al principio todos los botones están rojos. ¿Es posible, oprimiendo sucesivamente algunos botones, lograr que todas las luces queden verdes? hay un botón, que puede estar de color rojo o verde. Si se oprime un botón en el borde del tablero, él y todos sus vecinos cambian de color. Si se oprime el botón central, cambian de color sus ocho vecinos, pero él mantiene su color. Al principio todos los botones están rojos. ¿Es posible, oprimiendo sucesivamente algunos botones, lograr que todas las luces queden verdes?Problema 5: La figura muestra un cuadrado de lado 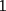 , que en su interior contiene un cuadrado de lado , que en su interior contiene un cuadrado de lado 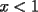 y una circunferencia de radio y una circunferencia de radio  , que es tangente a dos lados del cuadrado mayor y pasa por un vértice del cuadrado menor. Determine , que es tangente a dos lados del cuadrado mayor y pasa por un vértice del cuadrado menor. Determine  en función de en función de  . .Problema 6: Dado 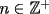 , sea , sea 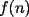 el promedio de sus divisores positivos. el promedio de sus divisores positivos.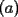 Pruebe que Pruebe que 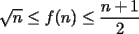 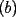 Encuentre todos los Encuentre todos los 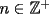 tales que tales que 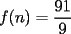 Resumen de soluciones Observación: la mayoría de estos ejercicios están ya resueltos en el foro, pero este topic va con la intención de ordenar... -------------------- Bachiller en Ciencias
(ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile  |
|
|
|
 |
Respuestas
 Sep 14 2006, 02:55 PM Sep 14 2006, 02:55 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La solución del problema 3 está impecable, sólo queda felicitar a Jaime sscc por conseguir una muy buena redacción de la solución del problema. En cuanto a la solución del problema 6, prefiero hacer algunos comentarios adicionales...
Por lo menos desde mi punto de vista, yo sé que la parte 1 tiene una solución bastante más corta de lo que tú hiciste. Entonces, al ver una solución tan larga, creo que es mejor resumirla antes de empezar a revisarla. Te sugiero que busques una solución más corta para esa parte Una ayuda sería encontrar una fórmula para el producto de todos los divisores de un número  , en términos de , en términos de  y de la cantidad de divisores de y de la cantidad de divisores de  . Sugiero que eso lo hagas aparte, antes de comenzar la demostración. O, simplemente, lo asumes como conocido. . Sugiero que eso lo hagas aparte, antes de comenzar la demostración. O, simplemente, lo asumes como conocido.Sobre la segunda parte, tengo sospechas mucho mayores, porque de 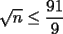 concluiste inmediatamente que concluiste inmediatamente que 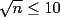 . Y después de eso, me ha quedado la impresión que asumiste que . Y después de eso, me ha quedado la impresión que asumiste que  es cuadrado perfecto. Por lo menos, ese es el trato que diste a es cuadrado perfecto. Por lo menos, ese es el trato que diste a  , y nunca diste un buen argumento para excluir a aquellos valores de , y nunca diste un buen argumento para excluir a aquellos valores de  que no son cuadrados perfectos. Así que la idea aquí es revisar tus propios argumentos. que no son cuadrados perfectos. Así que la idea aquí es revisar tus propios argumentos.
Mensaje modificado por Francisco Muñoz el Sep 15 2006, 12:34 AM -------------------- |
|
|
|
 Sep 14 2006, 11:25 PM Sep 14 2006, 11:25 PM
Publicado:
#3
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(xsebastian @ Sep 14 2006, 03:55 PM) La solución del problema 3 está impecable, sólo queda felicitar a Jaime sscc por conseguir una muy buena redacción de la solución del problema. En cuanto a la solución del problema 6, prefiero hacer algunos comentarios adicionales... Por lo menos desde mi punto de vista, yo sé que la parte 1 tiene una solución bastante más corta de lo que tú hiciste. Entonces, al ver una solución tan larga, creo que es mejor resumirla antes de empezar a revisarla. Te sugiero que busques una solución más corta para esa parte Una ayuda sería encontrar una fórmula para el producto de todos los divisores de un número  , en términos de , en términos de  y de la cantidad de divisores de y de la cantidad de divisores de  . Sugiero que eso lo hagas aparte, antes de comenzar la demostración. O, simplemente, lo asumes como conocido. . Sugiero que eso lo hagas aparte, antes de comenzar la demostración. O, simplemente, lo asumes como conocido.Sobre la segunda parte, tengo sospechas mucho mayores, porque de 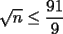 concluiste inmediatamente que concluiste inmediatamente que 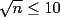 . Y después de eso, me ha quedado la impresión que asumiste que . Y después de eso, me ha quedado la impresión que asumiste que  es cuadrado perfecto. Por lo menos, ese es el trato que diste a es cuadrado perfecto. Por lo menos, ese es el trato que diste a  , y nunca diste un buen argumento para excluir a aquellos valores de , y nunca diste un buen argumento para excluir a aquellos valores de  que no son cuadrados perfectos. Así que la idea aquí es revisar tus propios argumentos. que no son cuadrados perfectos. Así que la idea aquí es revisar tus propios argumentos.Me comprometo a mañana terminar la parte 2. En la parte 1 tendría que buscar una solución más corta, pero igual la que está ahí es correcta Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
Mensajes en este tema
 Guía Rojo II OMCS (1991) Apr 19 2006, 07:07 PM
Guía Rojo II OMCS (1991) Apr 19 2006, 07:07 PM
 Killua Por fin me salió Francisco :victory:
$... Sep 6 2006, 11:44 PM
Killua Por fin me salió Francisco :victory:
$... Sep 6 2006, 11:44 PM
 Jaime sscc Problema 3:
\noindent$\displaystyl... Sep 7 2006, 09:16 PM
Jaime sscc Problema 3:
\noindent$\displaystyl... Sep 7 2006, 09:16 PM
 Francisco Muñoz Mucho tiempo despues de haberla posteado, cumplo ... Sep 15 2006, 01:08 AM
Francisco Muñoz Mucho tiempo despues de haberla posteado, cumplo ... Sep 15 2006, 01:08 AM
 Killua Parte 2 del P6 ahora editada, espero que esté bien... Sep 15 2006, 11:14 PM
Killua Parte 2 del P6 ahora editada, espero que esté bien... Sep 15 2006, 11:14 PM
 p.j.t [b]Problema 5: La figura muestra un cuadrado de la... Jan 22 2008, 05:47 PM
p.j.t [b]Problema 5: La figura muestra un cuadrado de la... Jan 22 2008, 05:47 PM
 makmat Con respecto al P6, si el numero de divisores del ... Sep 13 2008, 11:37 PM
makmat Con respecto al P6, si el numero de divisores del ... Sep 13 2008, 11:37 PM

 Felipe_ambuli Con respecto al P6, si el numero de divisores del ... Sep 14 2008, 01:29 PM
Felipe_ambuli Con respecto al P6, si el numero de divisores del ... Sep 14 2008, 01:29 PM

 makmat Para eso es util definir [tex=./tex/c35ef4c5dea306... Sep 17 2008, 12:18 AM
makmat Para eso es util definir [tex=./tex/c35ef4c5dea306... Sep 17 2008, 12:18 AM
 Hamon [b]Problema 4: En cada casilla de un tablero de [t... Jun 1 2010, 08:19 PM
Hamon [b]Problema 4: En cada casilla de un tablero de [t... Jun 1 2010, 08:19 PM

 makmat Vemos que inicialmente hay 9 botones rojos, que es... Jun 1 2010, 08:45 PM
makmat Vemos que inicialmente hay 9 botones rojos, que es... Jun 1 2010, 08:45 PM
 Hamon ajja suena bonito lo del "training Cono Sur... Jun 3 2010, 06:33 PM
Hamon ajja suena bonito lo del "training Cono Sur... Jun 3 2010, 06:33 PM
 Niklaash Solucion P1:
(*) [spoiler] (segun la figura) [t... Nov 17 2013, 05:11 PM
Niklaash Solucion P1:
(*) [spoiler] (segun la figura) [t... Nov 17 2013, 05:11 PM
 Kaissa Buena solución, Niklaash.
Tengo una solución habl... Nov 18 2013, 12:15 AM
Kaissa Buena solución, Niklaash.
Tengo una solución habl... Nov 18 2013, 12:15 AM
 Niklaash Buena solución, Niklaash.
Tengo una solución habl... Nov 18 2013, 01:31 PM
Niklaash Buena solución, Niklaash.
Tengo una solución habl... Nov 18 2013, 01:31 PM  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 10th April 2025 - 06:32 PM |










