Cuarto Nivel Individual

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2006 > Segunda Fecha

Cuarto Nivel Individual

Opciones

0.9999999...=1 Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 05:24 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 281 Registrado: 7-April 06 Desde: Santiago - Quirihue Miembro Nº: 786 Nacionalidad: Sexo:	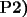$TEX: \textbf{P2)}$ Encuentre una fórmula en terminos de n para el valor de la suma $TEX: \[<br />\frac{2}{{3 + 1}} + \frac{{2^2 }}{{3^2 + 1}} + \frac{{2^3 }}{{3^4 + 1}} + \frac{{2^4 }}{{3^8 + 1}}... + \frac{{2^{n + 1} }}{{3^{2^n } + 1}}<br />\]$ Yo solo llegue a la conclusión k la sumatoria tendia a uno, esta bueno eso??, ojala, pa kme den algo de puntaje, jajajaja -------------------- "Si le das a un hombre un pescado, comerá un día. Si le enseñas a pescar, comerá toda la vida." "Si persiges a dos conejos al mismo tiempo, los perderás a ambos." "Las cosas valen lo que su comprador esté dispuesto a pagar por ellas."

Respuestas

†Alucard† Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 05:56 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 519 Registrado: 22-April 06 Desde: Concepción Miembro Nº: 925 Nacionalidad: Sexo:	Esto fue lo que yo hice: Lema 1: $TEX: \[<br />3^{2^{n + 1} } - 2\prod\limits_{i = 0}^n {(3^{2^i } + 1)} = 1<br />\]$ Para n=0 es verdadero (9-8=1), y si es cierto para algún n, multiplicándolo por $TEX: \[<br />3^{2^{n + 1} } + 1<br />\]$ : $TEX: \[<br />3^{2^{n + 2} } + 3^{2^{n + 1} } - 2\prod\limits_{i = 0}^{n + 1} {(3^{2^i } + 1)} = 3^{2^{n + 1} } + 1 \Rightarrow 3^{2^{n + 2} } - 2\prod\limits_{i = 0}^{n + 1} {(3^{2^i } + 1)} = 1<br />\]$ QED Lema 2: $TEX: \[<br />\frac{2}<br />{{3 + 1}} + \frac{{2^2 }}<br />{{3^2 + 1}} + \ldots + \frac{{2^{n + 1} }}<br />{{3^{2^n } + 1}} = 1 - \prod\limits_{i = 0}^n {\frac{2}<br />{{3^{2^i } + 1}}} <br />\]$ Para n=0 es verdadero ( 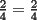$TEX: $\frac{2}{4}=\frac{2}{4}$$ ), y si es cierto para algún n, tenemos $TEX: \[<br />\begin{gathered}<br /> \frac{2}<br />{{3 + 1}} + \frac{{2^2 }}<br />{{3^2 + 1}} + \ldots + \frac{{2^{n + 2} }}<br />{{3^{2^{n + 1} } + 1}} \hfill \\<br /> = 1 - \prod\limits_{i = 0}^n {\frac{2}<br />{{3^{2^i } + 1}}} + \frac{{2^{n + 2} }}<br />{{3^{2^{n + 1} } + 1}} \hfill \\<br /> = 1 - 2^{n + 1} \left( {\frac{{3^{2^{n + 1} } + 1 - 2\prod\limits_{i = 0}^n {(3^{2^i } + 1)} }}<br />{{\prod\limits_{i = 0}^{n + 1} {(3^{2^i } + 1)} }}} \right) = 1 - 2^{n + 1} \left( {\frac{2}<br />{{\prod\limits_{i = 0}^{n + 1} {(3^{2^i } + 1)} }}} \right) = 1 - \prod\limits_{i = 0}^{n + 1} {\frac{2}<br />{{3^{2^i } + 1}}} \hfill \\ <br />\end{gathered} <br />\]$ (Nótese que usamos el lema 1 en la penúltima igualdad) QED Lema 3: $TEX: \[<br />\prod\limits_{i = 0}^n {(3^{2^i } + 1) = \frac{{3^{2^{n + 1} } - 1}}<br />{2}} <br />\]$ Para n=0 es verdadero (4=4), y si es cierto para algún n, entonces, multiplicándolo por $TEX: \[<br />3^{2^{n + 1} } + 1<br />\]$ , queda $TEX: \[<br />\prod\limits_{i = 0}^{n + 1} {(3^{2^i } + 1)} = \frac{{3^{2^{n + 2} } - 3^{2^{n + 1} } + 3^{2^{n + 1} } - 1}}<br />{2} = \frac{{3^{2^{n + 2} } - 1}}<br />{2}<br />\]$ QED Entonces: $TEX: \[<br />\frac{2}<br />{{3 + 1}} + \frac{{2^2 }}<br />{{3^2 + 1}} + \ldots + \frac{{2^{n + 1} }}<br />{{3^{2^n } + 1}} = 1 - \prod\limits_{i = 0}^n {\frac{2}<br />{{3^{2^i } + 1}}} = 1 - \frac{{2^{n + 1} }}<br />{{\frac{{3^{2^{n + 1} } - 1}}<br />{2}}} = 1 - \frac{{2^{n + 2} }}<br />{{3^{2^{n + 1} } - 1}}<br />\]$ (Usamos el lema 2 en la primera igualdad y el 3 en la siguiente) Lo que resuelve el problema Saludos -------------------- There is a theory which states that if ever anyone discovers exactly what the Universe is for and why is it here, it will instantly disappear and be replaced by something even more bizarre and inexplicable. There is another theory which states that this has already happened. - Adams, The Restaurant at the End of the Universe ----------------------------------- Existe una teoría que postula que si alguien alguna vez llega a descubrir exactamente para qué es el Universo y por qué está aquí, éste desaparecerá instantáneamente y será reemplazado por algo aún más extraño e inexplicable. Existe otra teoría que dice que esto ya ha ocurrido. - Adams, el Restorán al Final del Universo

Mensajes en este tema

0.9999999...=1 Cuarto Nivel Individual May 20 2006, 05:24 PM

†Alucard† Problema 1 En el año 2100, nuestra agencia espaci... May 20 2006, 05:37 PM

†Alucard† Esto fue lo que yo hice: Lema 1: \[ 3^{2^{n ... May 20 2006, 05:56 PM

0.9999999...=1 Supuestamente este signo \[ \prod {} ... May 20 2006, 06:12 PM

.r0 es parecido al de sumatoria, pero debes multiplica... May 20 2006, 06:26 PM

0.9999999...=1 Yo a ese le puse k siempre existia un planeta X k ... May 20 2006, 06:55 PM

Killua No es jugo, va en serio... ¿Por qué postean las pr... May 20 2006, 08:10 PM

†Alucard† Nota: No es que este post no tenga sentido, es sól... May 20 2006, 08:52 PM

Hexe pi..pi..ta..to..ri..a... q es eso??? que otra fo... May 20 2006, 09:03 PM

†Alucard† No sé, cuando llegué ya estaba este topic, y si s... May 20 2006, 09:33 PM

Kenshin Aqui les dejo algunas pistas para que puedan resol... May 20 2006, 09:42 PM

†Alucard† :buah_2: :buah_2: :buah_2: :buah_2: :buah_2... May 20 2006, 09:49 PM

Kenshin Por supuesto que puedes sentirte orgulloso de tu ... May 20 2006, 10:19 PM

Cesarator xsebastian Ese consejo es mágico, gracias a eso rescaté 29 p... May 20 2006, 10:45 PM
†Alucard† Bueno, siguiendo los Hints de Kenshin, tengo la nu... May 20 2006, 10:50 PM
Cesarator Es necesaria la demostración por inducción? May 20 2006, 10:54 PM
†Alucard† :oops: Yo siempre lo creí así... :jpt_blush: ... May 20 2006, 10:58 PM
pame_janita :buah_2: :buah_2: :buah_2: :buah_2: :buah_2... May 22 2006, 11:02 PM
0.9999999...=1 ahhhh, k wena k sacaras 20 ptos, entonces tu eres ... May 20 2006, 10:28 PM
Cesarator je je, lindo problema. Sólo 2 comentarios. La s... May 20 2006, 10:33 PM
Cesarator ... sentarse a reflexionar entonces :aporte: May 20 2006, 11:08 PM
Sasuke7410 Esto es lo q yo respondi hoy en el campeonato espe... May 20 2006, 11:12 PM
Cesarator Sasuke, una de las buenas cosas de postear en el f... May 20 2006, 11:26 PM
AsDf http://www.fmat.cl/tex/6686... May 21 2006, 09:32 AM
tt14123 P2) $$\frac{2}{3+1}+\frac{2^2... May 23 2006, 06:14 PM
Guía Rojo :condoro: no se entiende ni @&$)&%?... May 23 2006, 06:28 PM
tt14123 Ahi si esta Editado, perdon por el :condoro: , oj... May 23 2006, 09:24 PM
Kenshin Una nueva idea para el P2) http://www.fmat.cl/inde... Jun 17 2006, 11:16 PM

« Posterior · Segunda Fecha · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Cambiar a: Estándar · Cambiar a: Lineal+ · Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi Fecha y Hora actual: 23rd April 2025 - 12:10 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.